Batch Normalization
Batch Normalization
0. Introduction
0.1. Gradient Vanishing / Exploding
- Neural Network의 Train시에 Gradient 값의 변화를 보고 Parameter를 조절합니다.
- Gradient는 변화량, 즉 미분값입니다. Neural Network의 깊이가 깊어질수록 Backpropagation시에 Gradient 값들이 Input Layer의 입력값의 변화를 적절하게 학습에 반영하지 못합니다.
- Backpropagation시에, Non-Linear Activation Function(Ex. Sigmoid / Tanh )들을 사용하면 Layer를 지날수록 Gradient 값들이 점점 작아지거나(Gradient Vanishing) 혹은 반대로 Gradient 값들이 점점 커져서(Gradient Exploding), Input Layer의 변화량에 따른 Output Layer의 변화량을 Neural Network의 Parameter에 제대로 반영을 하지 못하는 상황이 발생합니다.
- 이 문제를 개선하기 위해서 몇가지 방법들이 제시되었습니다.
0.2. Countermeasure of Gradient Vanishing / Exploding
-
ReLU 사용
근본적인 원인이 Non Linear Activation Function을 사용했기 때문에, Linear Activation Function인 ReLU를 사용하는 방법입니다.
-
Special Weight Initialization
Layer의 Weight 값을 초기화를 잘하면 이 문제를 개선할 수 있다고 알려져 있습니다. He Initialization 혹은 Xavier Initialization이 잘 알려진 Weight Initialization 방법들입니다.
- 작은 Learning Rate 사용
0.3. Fundamental Solution
- 위에서 언급한 방법들은 모두 간접적으로 Gradient Vanishing / Exploding를 개선하는 방법들입니다.
- 근본적인 해결 방안을 연구하다가 나온 것은 Batch Normalization입니다.
1. Batch Normalization
- Batch Normalization이 소개된 Paper의 제목은 ‘Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift’입니다.
-
Paper의 Link는 여기를 참조해 주시기 바랍니다.
1.1. Advantage of Batch Normalization
알려진 Batch Normalization장점은 다음과 같습니다.
-
학습 속도가 빨라집니다.
가장 큰 장점이기도 합니다. 성능은 Batch Normalization을 적용하지 않는 것과 동일 혹은 더 좋아지면서도 적은 Epoch으로도 빠르게 수렴합니다. 어떤 분은 최소 10배 이상 빨라진다고 하네요.
-
Network의 Hyper Parameter에 대한 민감도가 감소합니다.
성능이 잘 나오지 않을 때 열심히 Hyper Parameter Tuning을 했는데, 이제 그것에 대한 부담을 크게 줄일 수 있습니다.
-
일반화(Regularization) 효과가 있습니다.
Inference 시에 성능이 더 좋아집니다.
1.2. Adding Batch Normalization Layer
- Batch Normalization Layer은 아래 그림과 같이 Hidden Layer 중간에 넣어주면 됩니다.
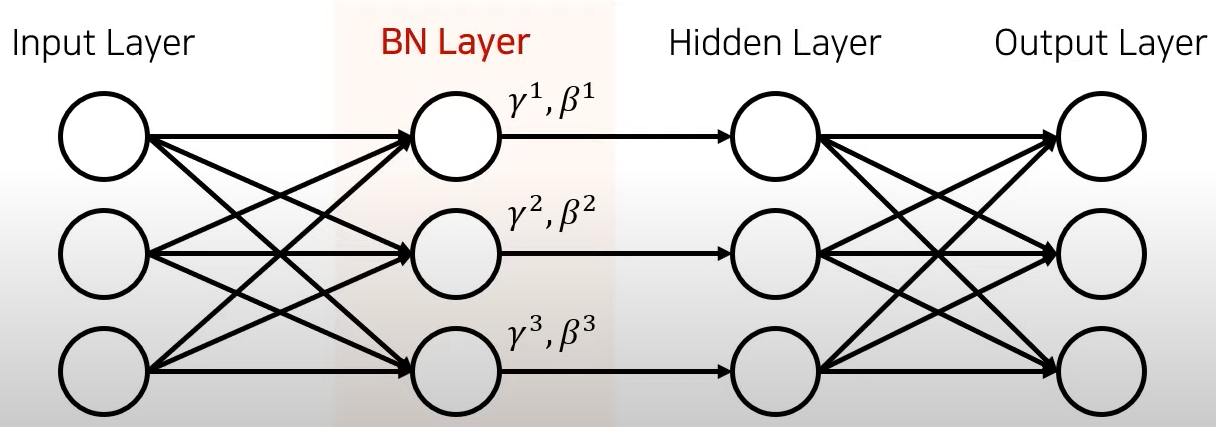
- 조금 더 구체적으로, Activation Function 앞에 넣어주는 것이 실험적으로 결과가 더 좋다고 합니다.
- 이전 Layer의 출력 Neuron의 수 만큼 γ, β 2개의 Parameter를 추가하여, 이전 Layer의 출력값을 다음 Layer에 넘기기 전에 적절하게 Control하는 것이 Batch Normalization의 핵심입니다.
- 2개 Parameter를 계산하는 비용만 추가하면 Network의 성능이 비약적으로 상승하기 때문에 사용하지 않을 이유가 없습니다.
2. Background
2.1. Normalization(정규화)
- 각 Feature들이 비슷한 범위의 값을 가지도록 하는 Normalization 기법은 많은 분야에서 사용되고 있으며, 이는 Training Speed를 향상시킵니다.
- Normalization을 하면 Training Speed가 빨라지는 이유는 각 Feature 별로 Variance가 다르면 큰 Learning Rate를 사용하기 어렵기 때문에 Training Speed를 빠르게 할 수 없다.
2.2. Standardization(표준화)
- Normalization(정규화)와 비슷한 방식이 Standardization(표준화)가 있습니다.
- Feature들의 분포를 평균 0, 분산 1로 만드는 방법입니다.
3. Implementation of Batch Normalization
- 최초 Input Layer에 Normalized 된 Feature를 넣는 것은 간단합니다. 전처리 과정에서 Normalization해서 입력하면 됩니다.
- 하지만, Hidden Layer의 입력분포가 매번 달라지고 정규화 되지 않는다면 Train이 잘 되지 않습니다.
- 그렇다면, 각 Hidden Layer마다 Normalized Feature Input은 어떻게 하면 될까요? 가장 간단하고 무식하게 각 Hidden Layer에 넘기기 전에 Normalization하면 됩니다.
3.1. Batch Normalization
- 아래 수식은 Paper에 나와있는 Batch Normalization의 Input값과 Output 값들의 계산 방법입니다.

-
1 : 우선 Batch Normalization에 Input으로 들어오는 값들에 대해서 알아보겠습니다.
mini-batch가 들어오는 데, x1 ~ xm 만큼 Input으로 들어오는데, 여기서 m은 Batch Size라고 생각하면 됩니다. 좀 더 구체적으로 이전 Layer의 Activation 출력값이 되겠지요.
- 2 : 이 γ, β 2개의 값이 우리가 실제로 학습해야할 값들입니다. 이 값들로 다음 Layer에 들어갈 값들을 Control하는 것입니다. 입력값 각각 마다 2개의 γ, β를 가지게 됩니다.
- 3 : mini-batch의 평균값을 구하는 과정입니다.
- 4 : mini-batch의 분산값을 구하는 과정입니다.
- 5 : Normalize 과정입니다.
- 6 : 0으로 나뉘는 것을 방지하기 위해서 아주 작은 값을 더해줍니다.
- 7 : 최종적으로 Batch Normalization을 거친 출력값입니다.
- γ,(Scale 역할) , β(Bias 역할)는 Neural Network 성능이 향상되는 방향(Loss가 작아지는 방향)으로 학습이 진행되는 과정을 거칩니다.
4. Effect of Batch Normalization
- Batch Normalization으로 얻을 수 있는 효과는 논란의 여지가 없습니다.
- 앞서 말했듯이, Train Speed가 빠르며 Hyper Parameter Tuning으로부터 자유로와 집니다.
- 아래의 다양한 조건에서의 Train 결과를 보면, Batch Normalization을 사용한 경우가 확실히 Train Speed가 빠르며, 큰 Learning Rate를 사용해도 빠르게 수렴하는 것을 알 수 있습니다.

5. Algorithm of Training & Inference
- 이제 Paper에서 소개된 Train / Inference시의 Batch Normalization 적용법에 대해서 알아보도록 하겠습니다.
- Batch Normalization 적용시에 다른 Network과 다른 점이라면, Train시의 Network과 Inference시의 Network이 다르다는 점입니다.
- 다른 이유는 Train시에 사용된 Data의 평균과 분산이 Inference시의 Data의 평균과 분산이 다르기 때문입니다.

- 1 : 이 Algorithm의 최종 목적은 Batch Normalization이 적용된 Inference를 하기 위한 Network을 얻는 것입니다.
- 2 : 기존 Network에 Batch Normalization Layer를 추가하겠다는 의미입니다.
- 3 : Batch Normalization Layer가 추가된 상태에서 γ, β를 학습을 합니다.
- 4 : 학습을 마친 후에, Parameter를 고정 한 후에 이제부터는 Inference Mode로 Network을 바꿉니다.
- 5 : 몇 개의 Train용 Mini Batch를 이용해 평균 분산을 구합니다.
- 6 : Inference시에는 이동 평균값을 이용합니다.
6. Essence of Batch Normalization
- 이번에는 Batch Normalization이 어떤 원리로 이렇게 좋은 성능을 내는지 알아보도록 하겠습니다.
6.1. Covariate Shift ( 공변량 변화)
- Covariate Shift란 학습에 사용된 Data Distribution과 Test시에 사용된 Data Distribution이 변경되는 현상을 말합니다.
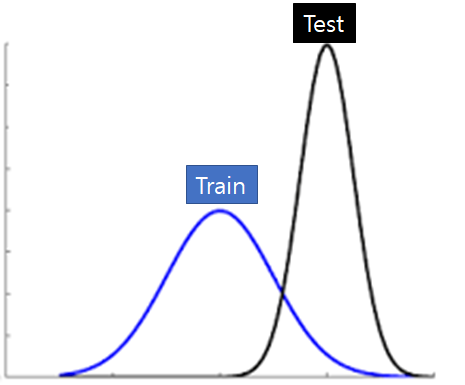
6.2. Internal Covariate Shift ( ICS )
- Internal Covariate Shift가 Network 내부에서 발생하는 현상을 의미하며, 이는 Batch Normalization이 최초 해결하고자 했던 문제입니다.
- 뒤쪽 Layer에서는 매번 Input Data Distribution이 달라진다는 것을 의미하며 Layer가 깊어질수록 이는 점점 더 심각해집니다.
- Batch Normalization이 발표된 이후에는 Batch Normalization의 성능 향상 요인이 ICS가 감소되기 때문이라고 알고 있었으나, 후속 연구에서 Batch Normalization의 효과가 ICS 감소와는 상관 없다는 주장이 제기됩니다.
-
Paper - How Does Batch Normalization Help Optimization?
6.3. Batch Normalization & Internal Covariate Shift ( ICS )
- Batch Normalization Layer 바로 다음에 Random Noise를 삽입하여 강제로 ICS를 발생시켜도 여전히 좋은 성능을 보여줍니다.

6.4. Smoothing Effect of Batch Normalization
- Batch Normalization는 Optimization Landscape를 부드럽게(Smoothing)하는 효과가 있습니다.
- Optimization Landscape란 Weight 따른 Loss의 변화를 시각화한 것입니다.
- 아래 그림이 Optimization Landscape인데, 왼쪽이 Batch Normalization을 적용하지 않는 것이고, 왼쪽이 Batch Normalization을 적용한 것입니다.
- 보시다시피, 왼쪽 Optimization Landscape의 경우, Weight Domain에서 Loss가 굉장히 들쑥날쑥 한 것을 확인할 수 있습니다.
- 반면에 오른쪽 Optimization Landscape의 경우, Loss값 분포가 매우 Smooth한 것을 알 수 있습니다.
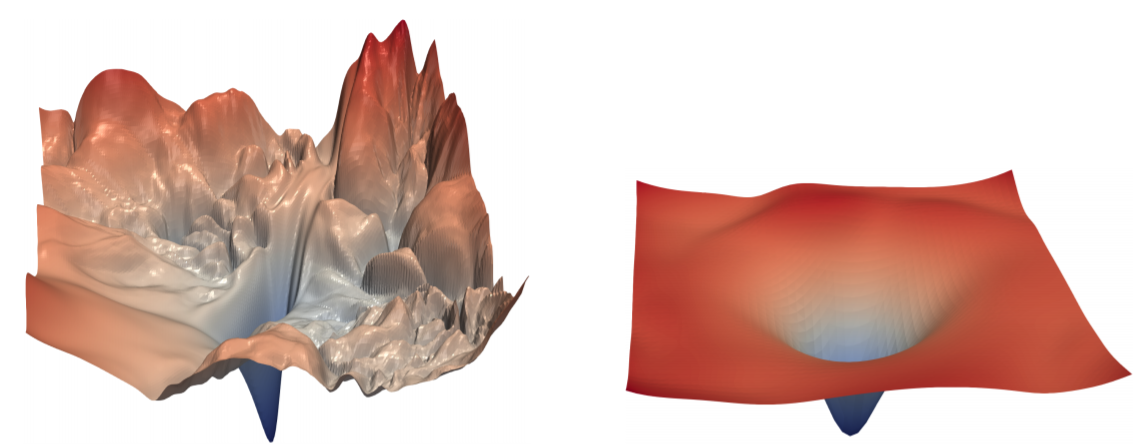
- 이런 Smoothing 효과가 있는 것은 Batch Normalization 뿐만 아니라, Residual Connection도 가지고 있다고 알려져 있습니다.
- Predictiveness(기울기 예측성)이란 현재의 기울기 방향성을 얼마나 신뢰할 수 있는 가를 나타내는 수치입니다.
- 첫번째 그림에서 Batch Normalization 적용시에는 Loss 자체의 변화가 작고, 많이 이동을 해도 Loss 변동이 크지 않습니다.
- 두번째 그림에서도 마찬가지로 큰 Step으로 기울기를 이동해도 많이 다르지 않습니다.
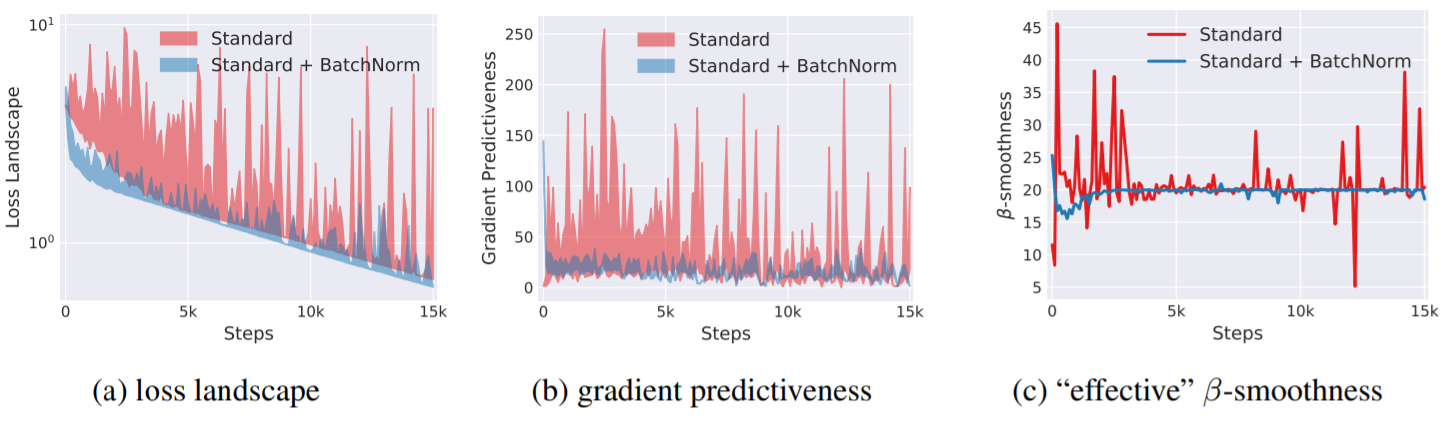
- 종합하면, Batch Normalization을 적용하면 현재의 기울기 방향으로 큰 Step만큼 이동을 해도 이동한 뒤의 기울기가 현재와 유사할 가능성이 높다는 의미입니다.