I like Machine Learning / Deep Learning.

4 minute read

GAN(Generative Adversarial Nets)







0. Introduction

  • 2014년에 Ian J. Goodfellow가 GAN(Generative Adversarial Nets)이라는 새로운 방식의 Model을 발표하였습니다.

  • 논문은 아래 Link에서 확인할 수 있습니다.

    Generative Adversarial Nets

  • ‘Nets’은 흔히 알고 있는 Network인 것은 알겠지만, Adversarial이나 Generative의 정확한 의미는 조금 어렵습니다.

  • 이번 Post에서는 GAN이 무엇인지 알아보도록 하겠습니다.





1. Background

1.1. Generative Model

  • GAN은 실제로 존재하지 않지만, 그럴싸한(있을법한) Data를 생성할 수 있는 Model의 종류를 말합니다.

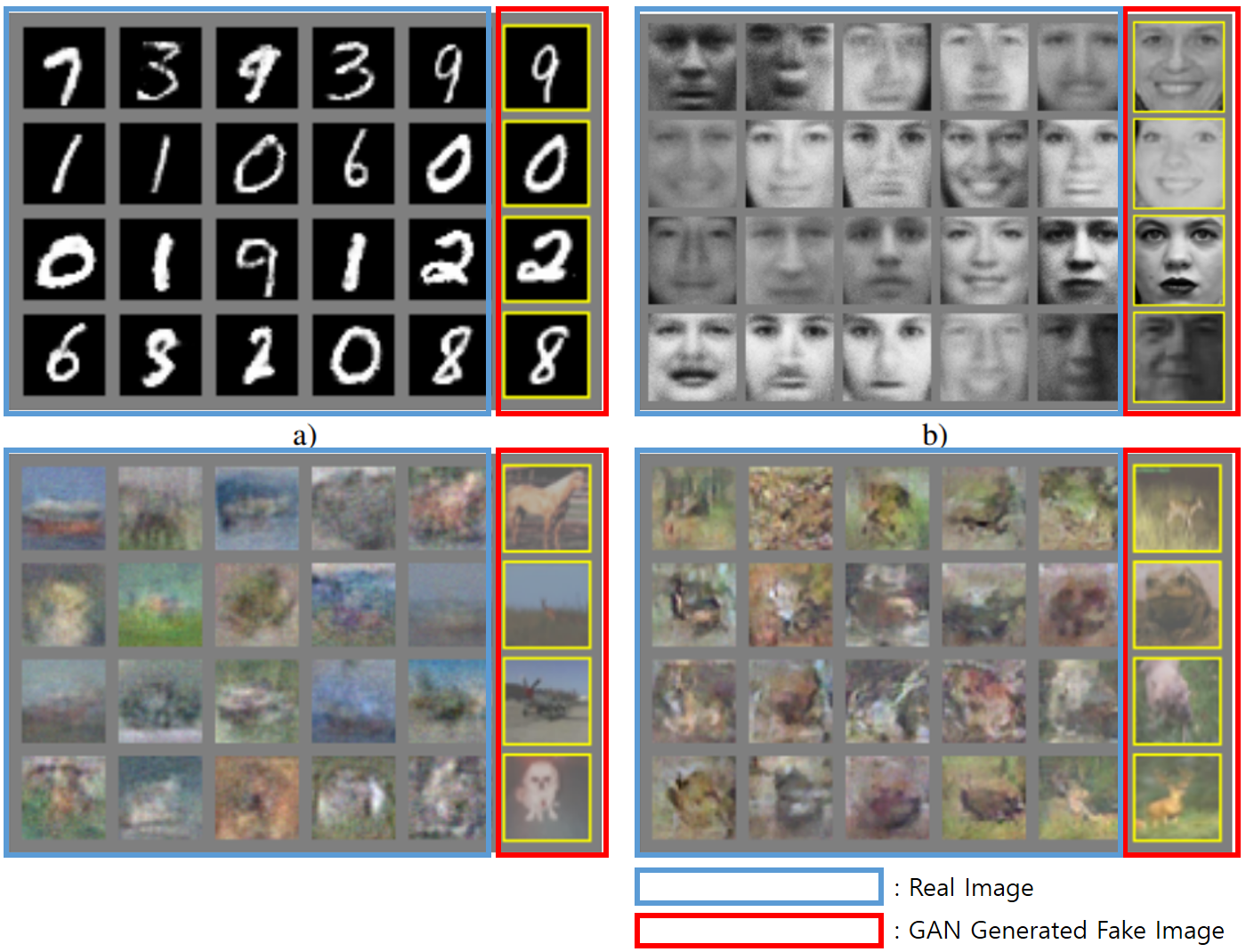
  • 아래 Image는 Ian Goodfellow의 Papaer에 나와있는 결과물입니다.

  • 파란색은 실제 Image Data이며, 빨간색은 GAN이 생성한 Image입니다. 정말 진짜 같네요.









1.2. Probability Distribution

  • 수학을 굉장히 싫어하지만, Paper의 내용이 모두 수식으로만 되어 있기 때문에 기본적인 지식을 가지고 Paper를 봐야할 것 같습니다.



  • 먼저 확률 분포(Probability Distribution)라는 개념을 알아봅시다.



  • Probability Distribution란 확률 변수가 특정한 값을 가질 확률을 나타내는 함수를 의미합니다.

    주사위를 던졌을 때 나올 수 있는 수를 확률변수 X라고 하면,

    P(X=1)은 1/6이며, P(X=1~6)까지 모두 같은 값(1/6)을 가집니다.



  • 확률 분포는 크게 2가지 종류, 이산확률분포(Discrete Probability Distribution), 연속확률분포(Continuous Probability Distribution)가 있습니다.





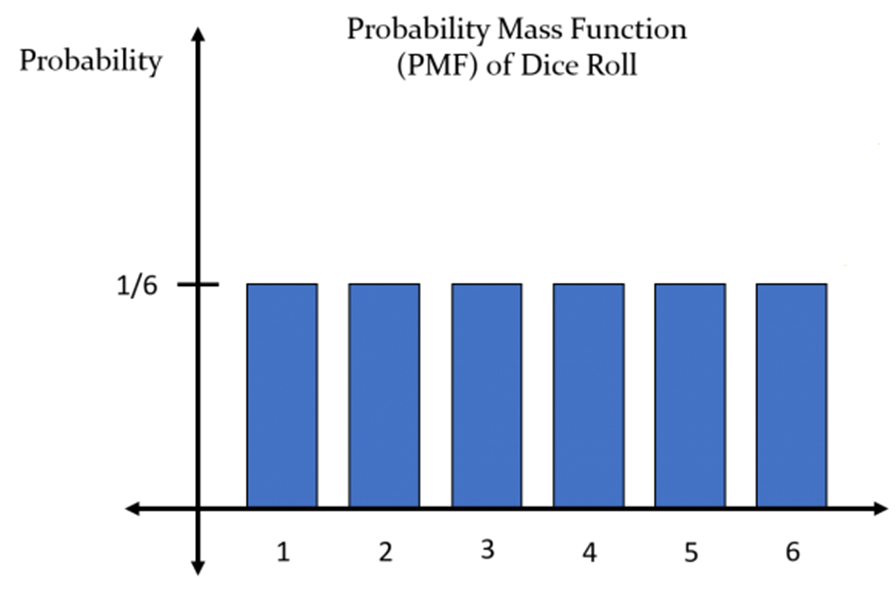
1.2.1. Discrete Probability Distribution

  • 이산확률분포란 확률 변수 X의 개수를 셀 수 있는 경우를 말합니다.


  • 앞에서 예를 든 주사위가 이산확률분포에 속합니다.





1.2.2. Continuous Probability Distribution

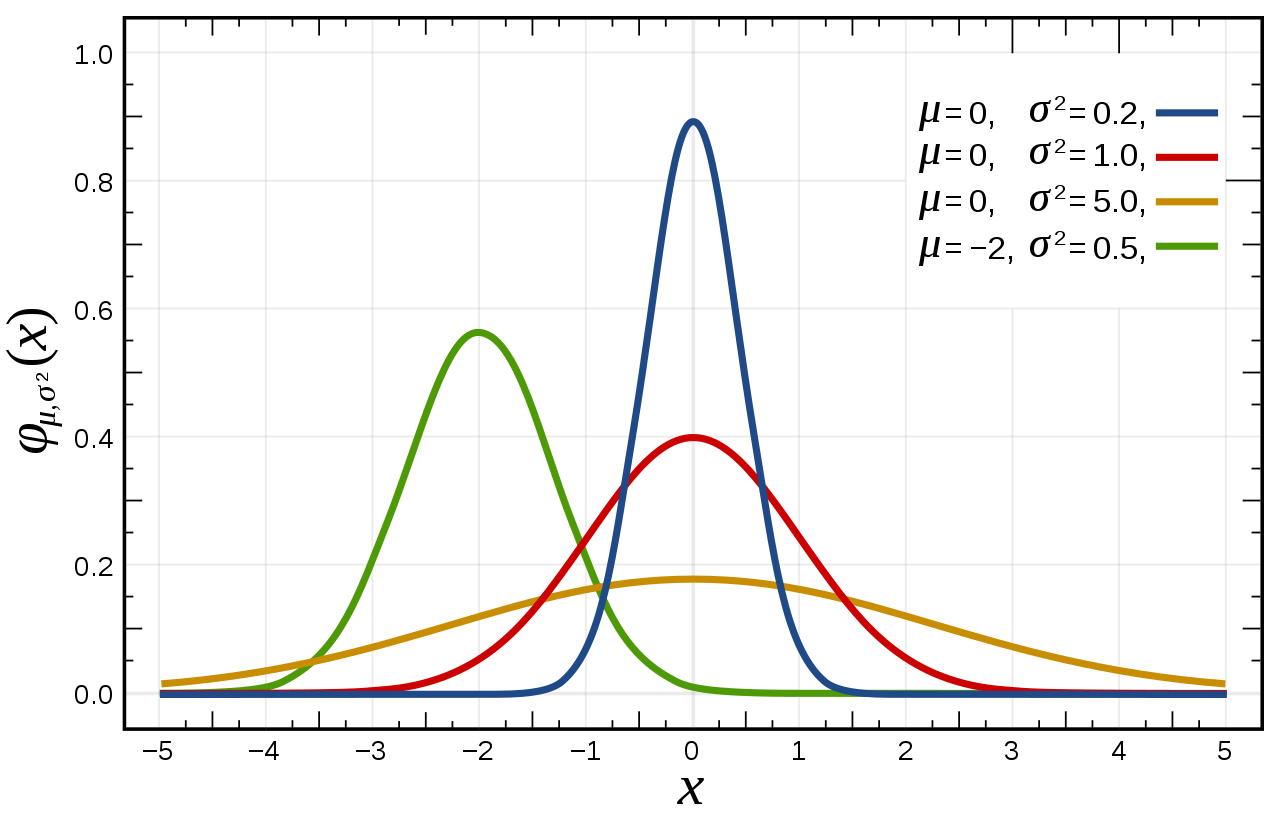
  • 연속확률분포는 확률 변수 X의 수를 정확하게 셀 수 없는 경우의 확률 분포입니다.


  • 확률 변수 X의 수를 정확하게 셀 수 없기 때문에 이 경우에는 확률 밀도 함수를 이용하여 확률 분포를 표현합니다.


  • 이런 경우의 예는 키 혹은 달리기 성적 등과 같은 것이 있을 수 있습니다.


  • 정규 분포도 연속 확률 분포라고 할 수 있습니다.




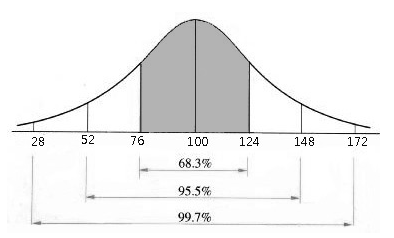
  • 실제로 현실에서는 많은 데이터의 분포를 정규분포로 근사화 할 수 있으며, 이러한 사실은 실제 Data 표현 및 활용에 매우 유용합니다.


  • 현실세계의 정규분포의 예로 IQ를 들 수 있습니다.






1.2.3. Probability Distribution of Image

  • Image에 대한 확률 분포라는 말이 다소 의아하게 생각될 수도 있습니다.


  • 생각해 보면, Image도 다차원 특징 공간의 한 점으로 표현될 수 있습니다. ( 고차원 Vector or Matrix )


  • 즉, Image Data를 확률 분포로 표현하여 이 확률 분포를 근사하는 Model을 GAN을 이용하면 학습할 수 있습니다.


  • ‘Image Data에 무슨 확률 분포가 있다는 말이지?’
    • 사람의 얼굴에는 통계적인 평균치가 있습니다.
    • 예를 들면, 눈,코,입 등의 상대적인 위치 등과 같은 값들이 있을 수 있겠죠.
    • 이런 수치들을 확률 분포로 표현할 수 있다는 의미입니다.


  • Image에서 다양한 특징들은 각각이 확률 변수가 될 수 있고, 이는 분포를 의미합니다.


  • 예를 들면 아래의 예시는 다변수 확률 분포(Multivariate Probability Distribution)를 나타냅니다.







2. 생성 모델(Generative Model)



2.1. Generative Model vs Discriminative Model

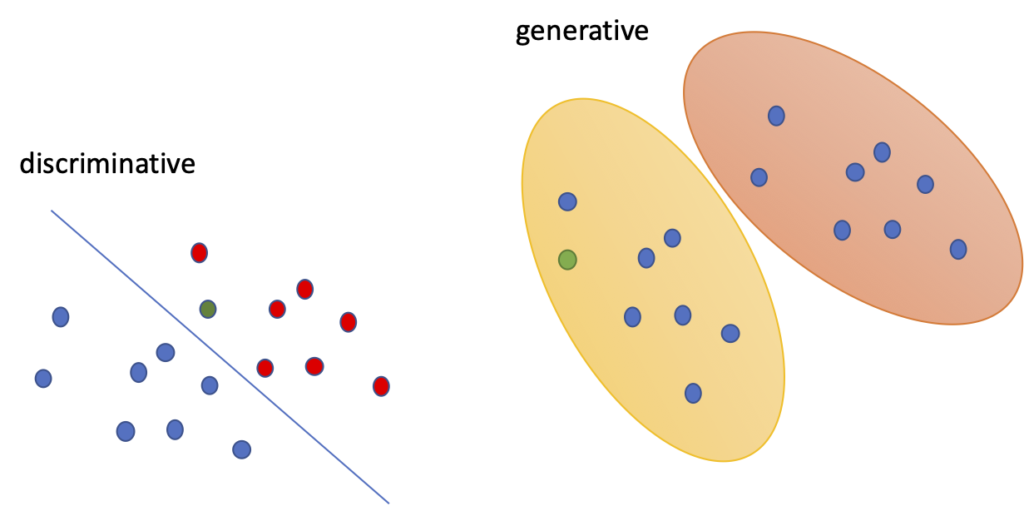
  • GAN 이전의 Machine Learning or Deep Learning Model들은 Data에서 Pattern을 학습하여 새로운 Data에 대해서 학습 결과를 바탕으로 Model이 특정 값을 출력하고, 이 값을 바탕으로 분류(discriminate)를 할 수 있도록 합니다.


  • 즉, Discriminative Model은 특정한 Decision Boundary를 학습하는 것입니다.


  • 이에 반해, 생성 모델은 확률 분포 Data를 학습하여 실제로는 존재하지 않지만, 학습한 확률 분포와 유사한 확률 분포를 생성하는 Model을 말합니다.


  • 즉, 생성 모델은 통계적인 평균치를 학습하고 이와 유사한 확률 분포를 생성한다는 의미입니다.




2.2. 생성 모델의 목표(Purpose of Generative Model)

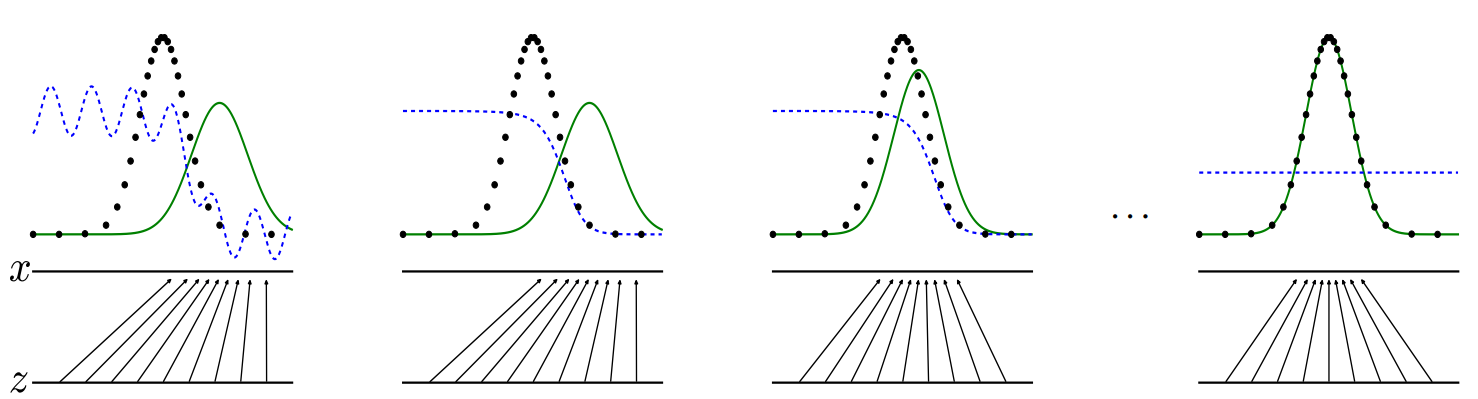
  • 앞에서 몇 번 언급한 바와 같이, 생성 모델의 목표는 확률 분포를 근사하는 모델 G를 생성하는 것입니다.


  • 생성 모델은 다음과 같은 과정으로 학습을 진행하며 원래 Data의 확률 분포를 근사화하도록 학습을 진행합니다.


  • G가 학습이 잘 이루어졌다면, 원본 Data와 통계적 평균이 유사한 Data를 쉽게 생성할 수 있을 것입니다.


  • 이 그래프의 좀 더 자세한 설명은 나중에 하도록 하겠습니다.







3. GAN(Generative Adversarial Nets)



  • 생성자(Generator)와 판별자(Discriminator), 2개의 Network을 활용한 생성 Model입니다.


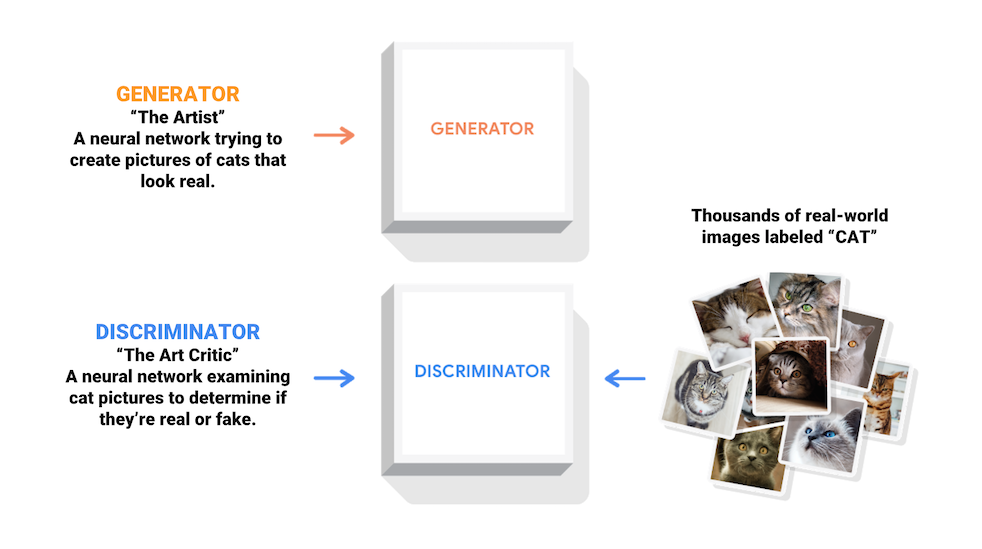
  • 아래 그림은 Tensorflow의 GAN Page에서 가져온 것이며, GAN의 기본적인 구조를 나타냅니다.


  • 크게 2가지의 Model, 생성자(Generator)와 판별자(Discriminator)가 있습니다.


  • Generator는 원본 Data 확률 분포를 학습하여 원본 확률 분포와 유사한 Data를 생성하는 방향으로 학습하고, Discriminator는 Generator가 생성하는 Data가 Real인지 Fake인지 구분을 잘하는 방향으로 학습합니다.


  • 이 2개의 Model이 경쟁적(Adversarial)으로 학습을 진행하여 최종적으로 Generator의 성능을 향상시키는 것이 목적입니다.




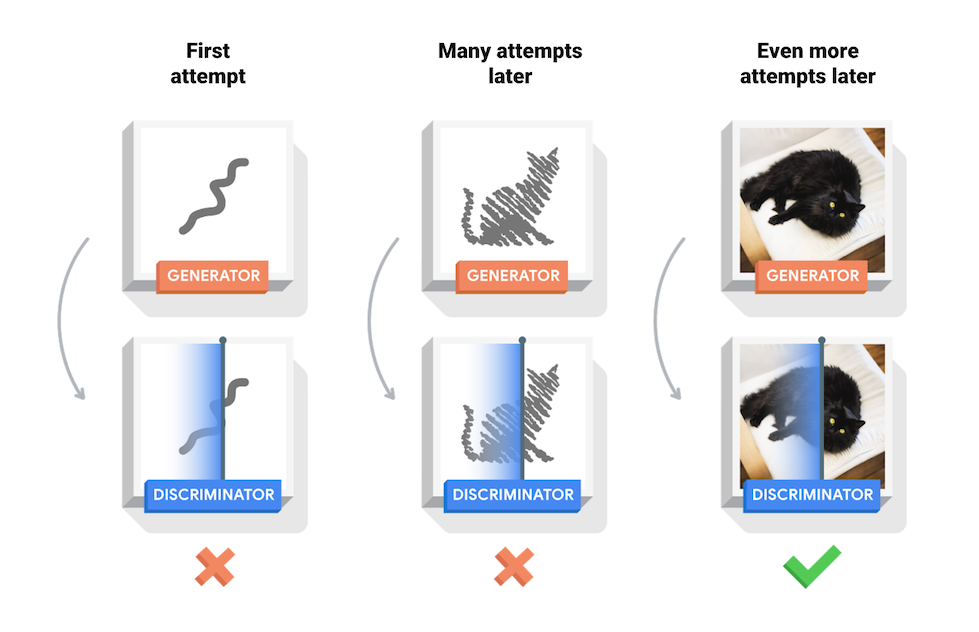
  • 훈련과정 동안 생성자는 점차 실제같은 이미지를 더 잘 생성하게 되고, 감별자는 점차 진짜와 가짜를 더 잘 구별하게됩니다. 이 과정은 감별자가 가짜 이미지에서 진짜 이미지를 더이상 구별하지 못하게 될때, 평형상태에 도달하게 됩니다.





  • 판별자(Discriminator)의 역할은 생성자 G가 학습을 잘 할 수 있도록 도와주는 역할이며, 최종적으로 얻으려는 것은 생성자(Generator , G)입니다.


  • 다음의 수식은 Ian의 Paper에 나오는 수식이며, GAN의 동작을 잘 설명하고 있습니다.




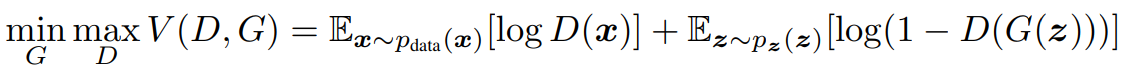
  • 위의 수식의 의미를 하나씩 알아보도록 하겠습니다.



  • #1 : 전체 함수 V는 D와 G로 구성되어 있다.


  • #2 : D는 전체 수식 V를 Maximize하려는 방향으로 학습한다.


  • #3 : 반대로 G는 전체 수식 V를 Minimize하려는 방향으로 학습한다.




  • 우선, D가 포함된 항부터 알아보겠습니다.



  • #1 : 확률 분포 P에서 Data 하나(x)를 꺼냅니다.


  • #2 : 꺼낸 Data(x)를 함수 D에 넣은 결과에 log를 취해서


  • #3 : 기대값(E)를 구한다는 의미입니다. 여기서 기대값이란 평균을 구한다고 생각하시면 됩니다.




  • G가 포함된 항을 알아보겠습니다.



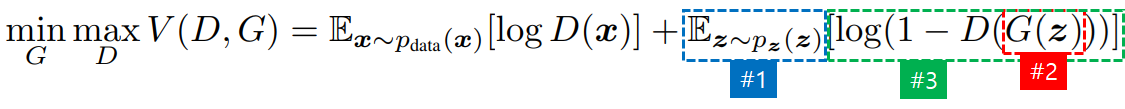
  • #1 : 확률 분포 z란 Latent Vector이며, Noise Vector입니다. Latent Vector에서 z를 하나 꺼냅니다.


  • #2 : z를 G에 넣어서 G가 생성한 값을 D에 넣은 결과를 1에서 뺀 후 log를 취합니다.


  • #3 : log를 취한 결과를 전체 기대값(평균)을 구합니다.




  • 위의 수식에서 G(z)는 Generator로써, Latent Vector z로부터 새로운 Data Instance를 생성합니다.


  • D(x)는 확률 분포 x가 Real인지 Fake인지 확률을 Return해 줍니다. ( Real : 1 , Fake : 0 )



  • V는 D와 G에 의해서 최적화 된다고 볼 수 있으며, 결과적으로 G는 그럴싸한 Data를 생성할 수 있을 것이라고 Paper에서는 이야기 하고 있습니다.




3.1. 기대값의 계산


  • 위의 수식에서 E(기대값) 계산을 하고 있는데, 실제 Code에서 구현하는 가장 간단한 방법은 단순히 모든 Data에 대해서 값을 구한 다음에 평균을 구하면 됩니다.


  • 보통 E(기대값)은 많은 Data를 다룰 때, 평균값을 구하고자 하는 경우에 사용합니다.



  • 위의 식은 원본 Data 분포에서 x를 뽑아서 logD(x)의 기대값을 계산하라는 의미입니다.





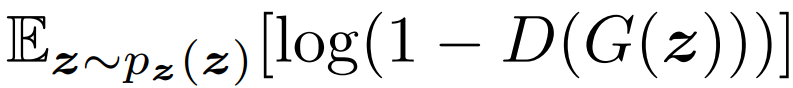
  • 위의 수식은 Latent Vector에서 z를 뽑아, log(1 - D(G(z)))의 기대값을 계산한다는 의미입니다.


  • 실제 Code에서는 반복문으로 모든 Data에 대해서 계산하면 됩니다.





3.2. 학습 과정



  • 학습의 목표는 다음 수식으로 설명된다.




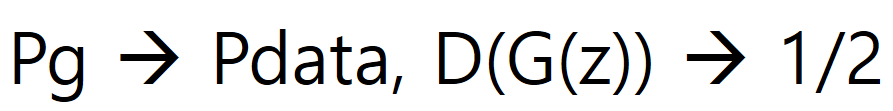
  • G가 학습이 끝나면 D는 G가 생성해낸 Real / Fake를 구분하지 못하기 때문에 확률을 1/2로 Return합니다.


  • 위의 수식의 증명은 Paper에 아주 복잡한 수식으로 증명되어 있으니, 참고하시기 바랍니다.



  • 학습 과정을 이전에 보여드렸던 그림으로 다시 보도록 하겠습니다.


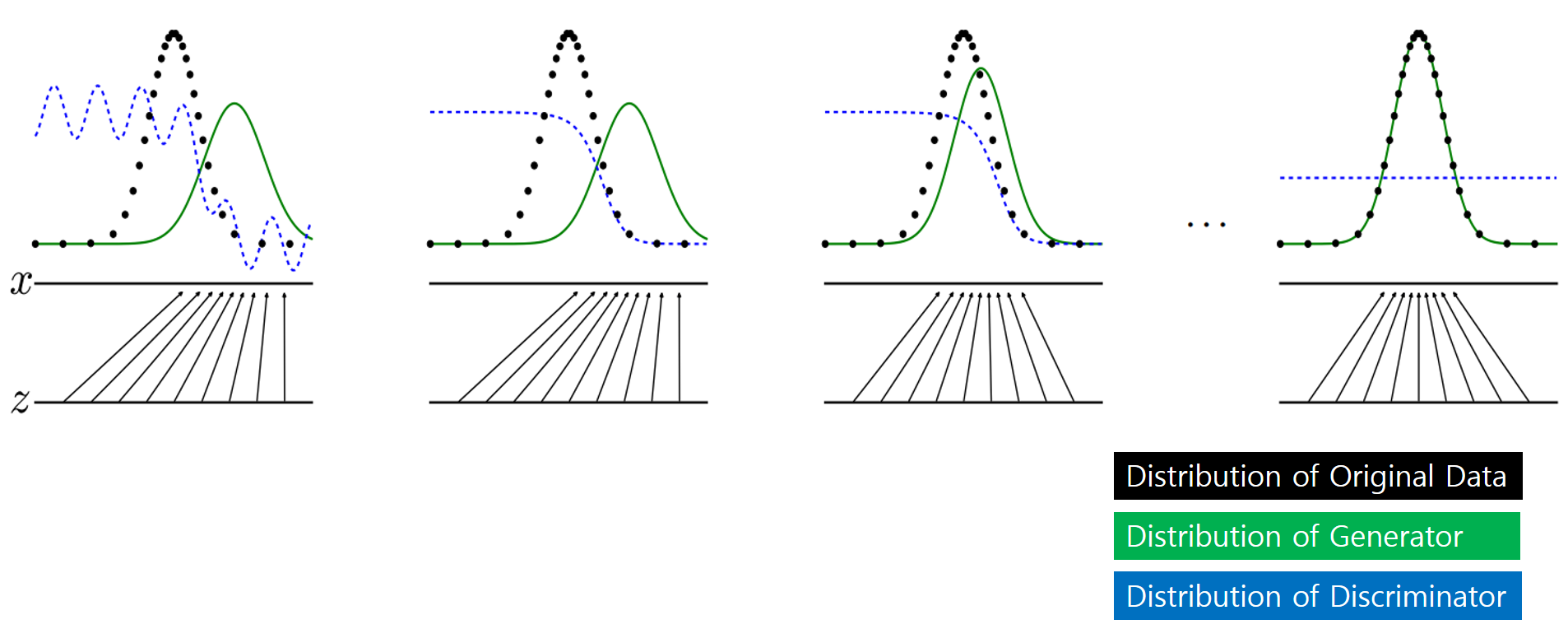
  • 검은색 확률 분포는 원본 Data의 확률 분포를 나타내고, 초록색은 Generator가 생성하는 확률 분포, 파란색은 Discriminator의 Return 값을 나타냅니다.


  • 왼쪽에서 오른쪽으로 학습이 진행될수록 생성 Model이 생성하는 확률 분포가 원본의 확률 분포를 따라가고, 판변 Model은 1/2로 수렴한다는 것을 나타냅니다.





3.3. GAN의 학습 알고리즘



  • 아래 Pseudo Code는 Paper에 나와있는 Code입니다.




  • 먼저 D(Discriminator)를 먼저 학습합니다.


  • m개의 Sample을 Latent Vector에서 추출하고, 원본 Data에서도 m개의 Sample을 추출합니다.


  • D는 기울기를 관찰하면서 중간에 있는 수식을 Maximize하는 방향으로 학습을 진행합니다.


  • 위와 같은 방법으로 D를 k번 반복 학습 합니다.


  • 그 다음에 G(Generator)를 학습합니다. m개의 Sample을 Latent Vector에서 추출합니다.


  • 아래쪽에 수식값을 Minimize하는 방향으로 학습을 진행합니다.




  • 이번 Post에서는 GAN Paper를 간단하게 Review해 보았습니다.


  • 다음 Post에서는 실제 Code를 실행해 보면서 GAN을 알아보도록 하겠습니다.

You May Also Enjoy