LSTM Exercise #01 - Airplane Passengers Prediction
LSTM Exercise #01 - Airplane Passengers Prediction
-
이번 예제에서는 LSTM을 이용하여 비행기 승객수 예측을 해 보도록 하겠습니다.
-
비교적 Data가 적지만, 예제로 사용하기에는 충분하다고 생각합니다.
0. 준비
-
필요한 Package들을 Load하고, 이런저런 설정을 합니다.
-
늘 그렇듯 Keras & Tensorflow를 사용하도록 하겠습니다.
#-*- coding: CP949 -*-
%matplotlib inline
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
import matplotlib
from IPython.display import set_matplotlib_formats
matplotlib.rc('font', family='Malgun Gothic')
matplotlib.rc('axes', unicode_minus=False)
set_matplotlib_formats('retina')
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
%config IPCompleter.greedy=True
import matplotlib.pyplot as plt
import math
import numpy as np
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
from keras.preprocessing.sequence import TimeseriesGenerator
Using TensorFlow backend.
-
우리가 사용할 Data를 Load하겠습니다.
- Download하실 분은 아래 Link를 참조해 주시기 바랍니다.
- Pandas가 CSV 읽기가 쉽기 때문에 먼저 Pandas로 Load합니다.
dataframe = pd.read_csv('airline-passengers.csv', usecols=[1], engine='python')
- 총 144개의 Data가 있고, 승객수를 저장한 하나의 Column만 있는 Simple한 Data입니다.
dataframe.head()
dataframe.tail()
dataframe.info()
| passengers | |
|---|---|
| 0 | 112 |
| 1 | 118 |
| 2 | 132 |
| 3 | 129 |
| 4 | 121 |
| passengers | |
|---|---|
| 139 | 606 |
| 140 | 508 |
| 141 | 461 |
| 142 | 390 |
| 143 | 432 |
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 144 entries, 0 to 143
Data columns (total 1 columns):
passengers 144 non-null int64
dtypes: int64(1)
memory usage: 1.2 KB
- Neural Net에 입력하기 위해서 Float Array로 변경하도록 하겠습니다.
dataset = dataframe.values
dataset = dataset.astype('float32')
dataset.shape
dataset
(144, 1)
array([[112.],
[118.],
[132.],
[129.],
[121.],
[135.],
[148.],
[148.],
[136.],
[119.],
[104.],
[118.],
[115.],
[126.],
[141.],
[135.],
[125.],
[149.],
[170.],
[170.],
[158.],
[133.],
[114.],
[140.],
[145.],
[150.],
[178.],
[163.],
[172.],
[178.],
[199.],
[199.],
[184.],
[162.],
[146.],
[166.],
[171.],
[180.],
[193.],
[181.],
[183.],
[218.],
[230.],
[242.],
[209.],
[191.],
[172.],
[194.],
[196.],
[196.],
[236.],
[235.],
[229.],
[243.],
[264.],
[272.],
[237.],
[211.],
[180.],
[201.],
[204.],
[188.],
[235.],
[227.],
[234.],
[264.],
[302.],
[293.],
[259.],
[229.],
[203.],
[229.],
[242.],
[233.],
[267.],
[269.],
[270.],
[315.],
[364.],
[347.],
[312.],
[274.],
[237.],
[278.],
[284.],
[277.],
[317.],
[313.],
[318.],
[374.],
[413.],
[405.],
[355.],
[306.],
[271.],
[306.],
[315.],
[301.],
[356.],
[348.],
[355.],
[422.],
[465.],
[467.],
[404.],
[347.],
[305.],
[336.],
[340.],
[318.],
[362.],
[348.],
[363.],
[435.],
[491.],
[505.],
[404.],
[359.],
[310.],
[337.],
[360.],
[342.],
[406.],
[396.],
[420.],
[472.],
[548.],
[559.],
[463.],
[407.],
[362.],
[405.],
[417.],
[391.],
[419.],
[461.],
[472.],
[535.],
[622.],
[606.],
[508.],
[461.],
[390.],
[432.]], dtype=float32)
- 실제로 이렇게 생긴 Data입니다.
plt.plot(dataset)
plt.show()

- Tree Base가 아닌 Neural Net에 입력하기 위해서는 수치를 Normalization해 주는 것이 성능에 좋습니다.
# normalize the dataset
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(dataset)
dataset
array([[0.01544401],
[0.02702703],
[0.05405405],
[0.04826255],
[0.03281853],
[0.05984557],
[0.08494207],
[0.08494207],
[0.06177607],
[0.02895753],
[0. ],
[0.02702703],
[0.02123553],
[0.04247104],
[0.07142857],
[0.05984557],
[0.04054055],
[0.08687258],
[0.12741312],
[0.12741312],
[0.10424709],
[0.05598456],
[0.01930502],
[0.06949806],
[0.07915059],
[0.08880308],
[0.14285713],
[0.11389962],
[0.13127413],
[0.14285713],
[0.18339768],
[0.18339768],
[0.15444016],
[0.11196911],
[0.08108109],
[0.1196911 ],
[0.12934363],
[0.14671814],
[0.17181468],
[0.14864865],
[0.15250966],
[0.22007722],
[0.24324325],
[0.26640925],
[0.2027027 ],
[0.16795367],
[0.13127413],
[0.17374519],
[0.17760617],
[0.17760617],
[0.25482625],
[0.25289574],
[0.24131274],
[0.26833975],
[0.3088803 ],
[0.32432434],
[0.25675675],
[0.20656371],
[0.14671814],
[0.18725869],
[0.19305018],
[0.16216215],
[0.25289574],
[0.23745173],
[0.25096524],
[0.3088803 ],
[0.38223937],
[0.36486486],
[0.2992278 ],
[0.24131274],
[0.1911197 ],
[0.24131274],
[0.26640925],
[0.24903473],
[0.31467178],
[0.3185328 ],
[0.32046333],
[0.4073359 ],
[0.5019305 ],
[0.46911195],
[0.40154442],
[0.32818535],
[0.25675675],
[0.3359073 ],
[0.34749034],
[0.33397684],
[0.41119692],
[0.4034749 ],
[0.4131274 ],
[0.52123547],
[0.5965251 ],
[0.58108103],
[0.484556 ],
[0.3899614 ],
[0.3223938 ],
[0.3899614 ],
[0.4073359 ],
[0.3803089 ],
[0.48648646],
[0.47104248],
[0.484556 ],
[0.6138996 ],
[0.6969112 ],
[0.70077217],
[0.57915056],
[0.46911195],
[0.38803086],
[0.44787642],
[0.45559844],
[0.4131274 ],
[0.4980695 ],
[0.47104248],
[0.49999997],
[0.6389961 ],
[0.7471043 ],
[0.7741313 ],
[0.57915056],
[0.492278 ],
[0.3976834 ],
[0.44980696],
[0.49420848],
[0.45945945],
[0.5830116 ],
[0.5637065 ],
[0.61003864],
[0.71042466],
[0.8571429 ],
[0.8783784 ],
[0.69305015],
[0.5849421 ],
[0.4980695 ],
[0.58108103],
[0.6042471 ],
[0.554054 ],
[0.60810804],
[0.6891892 ],
[0.71042466],
[0.8320464 ],
[1. ],
[0.96911204],
[0.7799227 ],
[0.6891892 ],
[0.55212355],
[0.6332046 ]], dtype=float32)
- Train에 사용할 Data와 Validation에 사용할 Data를 2:1의 비율로 나누도록 하겠습니다.
# split into train and test sets
train_size = int(len(dataset) * 0.67)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
train.shape
test.shape
(96, 1)
(48, 1)
1. TimeseriesGenerator
-
LSTM을 이용한 Time Series Regression을 시작하기 전에 Keras에서 제공해 주는 유용한 Class를 하나 소개해 드리고자 합니다.
-
LSTM을 이용해서 Supervised Time Series Prediction을 하려면 어찌되었던 (Train Value , Target) 형태의 값을 준비해야 합니다.
-
이전 LSTM Exer #00에서는 이런 형태의 Train Data를 만들기 위해서 임의의 Utility Function을 만들어서 사용했습니다.
-
Time Series Prediction Problem에서는 이러한 Data 생성이 비일비재하기 때문인지, Keras에서 전용 Class를 만들어 두었습니다.
-
이번 Exercise에서는 이 Class를 사용할 예정이어서 간단하게 사용법을 알아보도록 하겠습니다.
1.1. 사용방법
-
다음과 같은 형태의 Time Series Data가 있다고 가정해 봅시다.
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10] -
우리가 하고 싶은 것은 이 Data를 보고 다음 Data의 값을 예측하는 것입니다. ( 10 다음에는 무슨 값이 올까 ? )
-
TimeseriesGenerator의 정의를 잠시 살펴보겠습니다.
keras.preprocessing.sequence.TimeseriesGenerator(data, targets, length, sampling_rate=1, stride=1, start_index=0, end_index=None, shuffle=False, reverse=False, batch_size=128)
- data : 리스트 또는 NumPy 배열과 같이 인덱싱 가능한 2D 데이터로 0번째 축axis은 연속된 시점에 모인 표본sample들로 이루어진 시간 차원을 나타냅니다.
- targets : data의 시간 단계와 상응하는 목표값으로 0번째 축의 길이가 data와 서로 같아야 합니다.
- length : 생성할 배치의 시계열 길이를 지정합니다. 해당 인자를 통해 지정되는 길이는 최대 길이로서, 각 표본의 실제 길이는 length를 sampling_rate로 나눈 몫만큼이 됩니다.
- sampling_rate : length를 통해 지정된 시계열 범위 가운데 sampling_rate 시점마다 입력값을 추출해서 배치에 포함시킬 것인지를 정합니다. 예를 들어 표본이 i번째 데이터에서 시작할 때 sampling_rate를 r로 설정할 경우 생성되는 표본은 data[i], data[i+r], data[i+2r]… 의 형태가 되며, 표본의 최종 길이는 length를 sampling_rate로 나눈 몫이 됩니다. 기본값은 1이며, 이 경우 배치의 길이는 length와 같아집니다.
- stride : 입력값 가운데 stride로 지정한 순서마다 표본을 생성합니다. 예를 들어 첫번째 시계열 표본이 i번째 입력값에서 시작할 때 stride가 s면 다음 표본은 data[i+s]부터, 그 다음 표본은 data[i+2s]부터 생성됩니다. 표본 사이에 데이터가 중복되지 않게 하려면 stride값을 length보다 같거나 크게 지정하면 됩니다. 기본값은 1입니다.
- start_index : 입력값 가운데 배치 생성에 사용할 최초 시점을 지정합니다. start_index이전의 데이터는 사용되지 않기 때문에 별도의 시험/검증 세트를 만드는 데 활용할 수 있습니다. 기본값은 0입니다.
- end_index : 입력값 가운데 배치 생성에 사용할 마지막 시점을 지정합니다. end_index이후의 데이터는 사용되지 않기 때문에 별도의 시험/검증 세트를 만드는 데 활용할 수 있습니다. 기본값은 None으로, 이 경우 입력 데이터의 가장 마지막 인덱스가 자동으로 지정됩니다.
- shuffle : bool. True인 경우, 생성한 표본의 순서를 뒤섞습니다. 기본값은 False입니다.
- reverse : bool. True인 경우, 생성한 표본의 순서는 입력된 데이터의 역순입니다. 기본값은 False입니다.
- batch_size : 하나의 배치 안에 포함될 표본의 개수입니다. 기본값은 128입니다.
- Simple한 임의의 Time Series를 하나 정의해 보겠습니다.
input = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
- TimeseriesGenerator를 사용해 Train Data와 Target Value를 생성해 주는 Generator를 만들어 보겠습니다.
# length Option은 Time Steps라고 이해하시면 됩니다.
generator = TimeseriesGenerator(input, input, length=1, batch_size=1)
print(len(generator))
# Generator가 만들어 주는 값들을 확인해 보겠습니다.
for i in range(len(generator)):
x,y = generator[i]
print(x,y)
9
[[1]] [2]
[[2]] [3]
[[3]] [4]
[[4]] [5]
[[5]] [6]
[[6]] [7]
[[7]] [8]
[[8]] [9]
[[9]] [10]
- Time Steps를 2로 설정해 보겠습니다.
generator = TimeseriesGenerator(input, input, length=2, batch_size=1)
print(len(generator))
# Generator가 만들어 주는 값들을 확인해 보겠습니다.
for i in range(len(generator)):
x,y = generator[i]
print(x,y)
8
[[1 2]] [3]
[[2 3]] [4]
[[3 4]] [5]
[[4 5]] [6]
[[5 6]] [7]
[[6 7]] [8]
[[7 8]] [9]
[[8 9]] [10]
-
아주 예쁘게 Data Set을 만들어 줍니다.
-
엄밀히 말하면, Python의 Generator와는 성격이 약간 다르지만, 사용법은 매우 유사합니다.
-
이제 TimeseriesGenerator를 이용한 Train은 fit_generator로 사용하시면 됩니다.
-
예제로 한 번 살펴보도록 하겠습니다.
from numpy import array
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from keras.preprocessing.sequence import TimeseriesGenerator
# define dataset
series = array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
# reshape to [10, 1]
n_features = 1
series = series.reshape((len(series), n_features))
# define generator
n_input = 2
generator = TimeseriesGenerator(series, series, length=n_input, batch_size=8)
# define model
model = Sequential()
model.add(LSTM(128, activation='relu', input_shape=(n_input, n_features)))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')
# fit model
model.fit_generator(generator, steps_per_epoch=1, epochs=500, verbose=0)
# make a one step prediction out of sample
x_input = array([9, 10]).reshape((1, n_input, n_features))
yhat = model.predict(x_input, verbose=0)
print(yhat)
<keras.callbacks.History at 0x154f91f5688>
[[11.070835]]
- 훌륭합니다 ! 굉장히 편하네요.
2. LSTM Network for Regression
-
자, 이제 본격적으로 시작해 보도록 하겠습니다.
-
이번 Post에서 Alphabet Prediction과 유사하게, 다양한 방법으로 LSTM을 이용한 Regression을 해보도록 하겠습니다.
-
가장 먼저 살펴볼 방법은 단순하게, 이전 하나의 값을 보고 다음 값을 예측하도록 하는 Model을 만들어 보도록 하겠습니다.
-
이전 값을 하나만 살피는 것이므로, Time Steps는 1로 설정하도록 하고, Target은 그 다음에 오는 값으로 하는 Model을 만들어 보겠습니다.
-
Time Steps는 1로 설정합니다.
look_back = 1
- 앞에 설명드린 TimeseriesGenerator로 Train Data용 Generator를 만듭니다.
- 모양과 값을 한 번 살펴보도록 하죠.
train_generator = TimeseriesGenerator(train, train, length=look_back, batch_size=1)
len(train_generator)
for i in range(len(train_generator)):
x, y = train_generator[i]
print(x,y)
95
[[[0.01544401]]] [[0.02702703]]
[[[0.02702703]]] [[0.05405405]]
[[[0.05405405]]] [[0.04826255]]
[[[0.04826255]]] [[0.03281853]]
[[[0.03281853]]] [[0.05984557]]
[[[0.05984557]]] [[0.08494207]]
[[[0.08494207]]] [[0.08494207]]
[[[0.08494207]]] [[0.06177607]]
[[[0.06177607]]] [[0.02895753]]
[[[0.02895753]]] [[0.]]
[[[0.]]] [[0.02702703]]
[[[0.02702703]]] [[0.02123553]]
[[[0.02123553]]] [[0.04247104]]
[[[0.04247104]]] [[0.07142857]]
[[[0.07142857]]] [[0.05984557]]
[[[0.05984557]]] [[0.04054055]]
[[[0.04054055]]] [[0.08687258]]
[[[0.08687258]]] [[0.12741312]]
[[[0.12741312]]] [[0.12741312]]
[[[0.12741312]]] [[0.10424709]]
[[[0.10424709]]] [[0.05598456]]
[[[0.05598456]]] [[0.01930502]]
[[[0.01930502]]] [[0.06949806]]
[[[0.06949806]]] [[0.07915059]]
[[[0.07915059]]] [[0.08880308]]
[[[0.08880308]]] [[0.14285713]]
[[[0.14285713]]] [[0.11389962]]
[[[0.11389962]]] [[0.13127413]]
[[[0.13127413]]] [[0.14285713]]
[[[0.14285713]]] [[0.18339768]]
[[[0.18339768]]] [[0.18339768]]
[[[0.18339768]]] [[0.15444016]]
[[[0.15444016]]] [[0.11196911]]
[[[0.11196911]]] [[0.08108109]]
[[[0.08108109]]] [[0.1196911]]
[[[0.1196911]]] [[0.12934363]]
[[[0.12934363]]] [[0.14671814]]
[[[0.14671814]]] [[0.17181468]]
[[[0.17181468]]] [[0.14864865]]
[[[0.14864865]]] [[0.15250966]]
[[[0.15250966]]] [[0.22007722]]
[[[0.22007722]]] [[0.24324325]]
[[[0.24324325]]] [[0.26640925]]
[[[0.26640925]]] [[0.2027027]]
[[[0.2027027]]] [[0.16795367]]
[[[0.16795367]]] [[0.13127413]]
[[[0.13127413]]] [[0.17374519]]
[[[0.17374519]]] [[0.17760617]]
[[[0.17760617]]] [[0.17760617]]
[[[0.17760617]]] [[0.25482625]]
[[[0.25482625]]] [[0.25289574]]
[[[0.25289574]]] [[0.24131274]]
[[[0.24131274]]] [[0.26833975]]
[[[0.26833975]]] [[0.3088803]]
[[[0.3088803]]] [[0.32432434]]
[[[0.32432434]]] [[0.25675675]]
[[[0.25675675]]] [[0.20656371]]
[[[0.20656371]]] [[0.14671814]]
[[[0.14671814]]] [[0.18725869]]
[[[0.18725869]]] [[0.19305018]]
[[[0.19305018]]] [[0.16216215]]
[[[0.16216215]]] [[0.25289574]]
[[[0.25289574]]] [[0.23745173]]
[[[0.23745173]]] [[0.25096524]]
[[[0.25096524]]] [[0.3088803]]
[[[0.3088803]]] [[0.38223937]]
[[[0.38223937]]] [[0.36486486]]
[[[0.36486486]]] [[0.2992278]]
[[[0.2992278]]] [[0.24131274]]
[[[0.24131274]]] [[0.1911197]]
[[[0.1911197]]] [[0.24131274]]
[[[0.24131274]]] [[0.26640925]]
[[[0.26640925]]] [[0.24903473]]
[[[0.24903473]]] [[0.31467178]]
[[[0.31467178]]] [[0.3185328]]
[[[0.3185328]]] [[0.32046333]]
[[[0.32046333]]] [[0.4073359]]
[[[0.4073359]]] [[0.5019305]]
[[[0.5019305]]] [[0.46911195]]
[[[0.46911195]]] [[0.40154442]]
[[[0.40154442]]] [[0.32818535]]
[[[0.32818535]]] [[0.25675675]]
[[[0.25675675]]] [[0.3359073]]
[[[0.3359073]]] [[0.34749034]]
[[[0.34749034]]] [[0.33397684]]
[[[0.33397684]]] [[0.41119692]]
[[[0.41119692]]] [[0.4034749]]
[[[0.4034749]]] [[0.4131274]]
[[[0.4131274]]] [[0.52123547]]
[[[0.52123547]]] [[0.5965251]]
[[[0.5965251]]] [[0.58108103]]
[[[0.58108103]]] [[0.484556]]
[[[0.484556]]] [[0.3899614]]
[[[0.3899614]]] [[0.3223938]]
[[[0.3223938]]] [[0.3899614]]
- 우리가 원하는 형태로 잘 만들어져 있습니다.
- 추후에 Prediction을 위해서 미리 Validation Data Set도 Generator로 만들어 두도록 하겠습니다.
# Train 완료된 Model로 Predict
pred_generator = TimeseriesGenerator(test, test, length=look_back, batch_size=1)
- LSTM을 이용한 Model을 만들어보겠습니다.
- 이번 Exercise는 Regression이므로 Loss Function을 MSE로 설정하였습니다.
# create and fit the LSTM network
model = Sequential()
model.add(LSTM(16, input_shape=(look_back, 1)))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
- Generator를 사용하는 경우에는 fit대신 fit_generator라는 함수를 사용하여야 합니다.
- Epoch은 적당히 1000 정도로 하겠습니다.
# Train 시작
model.fit_generator(train_generator, steps_per_epoch=1, epochs=1000, verbose=2)
Epoch 1/1000
- 1s - loss: 0.0952
Epoch 2/1000
- 0s - loss: 0.0088
Epoch 3/1000
- 0s - loss: 0.0808
Epoch 4/1000
- 0s - loss: 0.0038
Epoch 5/1000
- 0s - loss: 0.0014
Epoch 6/1000
- 0s - loss: 0.0512
Epoch 7/1000
- 0s - loss: 0.1134
Epoch 8/1000
- 0s - loss: 0.0135
Epoch 9/1000
- 0s - loss: 0.0143
Epoch 10/1000
- 0s - loss: 0.0105
(중략)
Epoch 990/1000
- 0s - loss: 1.8631e-04
Epoch 991/1000
- 0s - loss: 9.0400e-05
Epoch 992/1000
- 0s - loss: 2.5155e-06
Epoch 993/1000
- 0s - loss: 1.4347e-05
Epoch 994/1000
- 0s - loss: 0.0010
Epoch 995/1000
- 0s - loss: 8.3244e-04
Epoch 996/1000
- 0s - loss: 0.0023
Epoch 997/1000
- 0s - loss: 8.7397e-04
Epoch 998/1000
- 0s - loss: 1.3480e-05
Epoch 999/1000
- 0s - loss: 4.7243e-05
Epoch 1000/1000
- 0s - loss: 2.4521e-04
<keras.callbacks.History at 0x154fcbc89c8>
import matplotlib.pyplot as plt
hist = model.history
fig, loss_ax = plt.subplots()
acc_ax = loss_ax.twinx()
loss_ax.plot(hist.history['loss'], 'y', label='train loss')
loss_ax.set_xlabel('epoch')
loss_ax.set_ylabel('loss')
loss_ax.legend(loc='upper left')
plt.show()

-
Train이 완료된 Model을 이용해서 Validation Data와 Train Data를 다시 Prediction 해 보겠습니다.
-
이렇게 하는 이유는 실제값과 어느 정도 비슷하게 Prediction하는지를 확인하기 위한 것과 RMSE(Root Mean Square Error)값도 구해보기 위함입니다.
test_pred = model.predict_generator( pred_generator )
train_pred = model.predict_generator( train_generator )
- Train 전에 Data를 Normalization했기 때문에 원래값으로 되돌리는 작업이 필요합니다.
test_pred = scaler.inverse_transform(test_pred)
train_pred = scaler.inverse_transform(train_pred)
- Validiation Data로 Model을 평가해 보겠습니다.
scores = model.evaluate_generator(pred_generator)
print("Look_back : %d - %s: %f" %(look_back, model.metrics_names[0], scores))
Look_back : 1 - loss: 0.012835
- Model이 얼마나 제대로 Prediction했는지 살펴보기 위해, 원래값과 예측값을 같은 그래프에 그려보겠습니다.
trainPredictPlot = np.empty_like(dataset)
trainPredictPlot[:, :] = np.nan
trainPredictPlot[look_back:len(train_pred)+look_back, :] = train_pred
testPredictPlot = np.empty_like(dataset)
testPredictPlot[:, :] = np.nan
testPredictPlot[len(train_pred)+(look_back*2)-1 :len(dataset)-1, :] = test_pred
# plot baseline and predictions
plt.plot(scaler.inverse_transform(dataset) , label='Original')
plt.plot(trainPredictPlot , label='Train Pred')
plt.plot(testPredictPlot , label='Test Pred')
plt.legend()
plt.show()

- 꽤 유사하게 추측한 것 같은데, 수치화해서 살펴보겠습니다.
- 얼마나 비슷하게 Prediction했는지 알아보기 위해서 RMSE를 구해보도록 하겠습니다.
trainY = []
testY = []
for i in range(len(train_generator)):
x, y = train_generator[i]
trainY.append( y[0][0] )
for i in range(len(pred_generator)):
x, y = pred_generator[i]
testY.append( y[0][0] )
trainY = np.reshape(trainY , (len(trainY), 1))
trainY = scaler.inverse_transform( trainY )
# calculate root mean squared error
trainScore = math.sqrt(mean_squared_error(trainY, train_pred))
print('Train Score: %f RMSE' % (trainScore))
testY = np.reshape(testY , (len(testY), 1))
testY = scaler.inverse_transform( testY )
testScore = math.sqrt(mean_squared_error(testY, test_pred))
print('Test Score: %f RMSE' % (testScore))
Train Score: 25.365068 RMSE
Test Score: 58.685135 RMSE
-
Train Set과 Validation Set에서의 RMSE 값입니다.
-
다른 방법들과 비교를 위한 Baseline 값으로 삼도록 하죠.
3. LSTM for Regression with Time Steps
- 이번에는 Time Steps를 주는 방법을 사용해 보도록 하겠습니다.
- LSTM이 원래 잘하는 것은 과거를 보고 미래를 예측하는 것입니다.
-
이런 의미에서 Time Steps를 주는 것이 LSTM을 잘 활용하는 방법입니다.
- Time Steps를 3으로 주도록 하겠습니다.
look_back = 3
train_generator = TimeseriesGenerator(train, train, length=look_back, batch_size=1)
len(train_generator)
for i in range(len(train_generator)):
x, y = train_generator[i]
print(x,y)
93
[[[0.01544401]
[0.02702703]
[0.05405405]]] [[0.04826255]]
[[[0.02702703]
[0.05405405]
[0.04826255]]] [[0.03281853]]
[[[0.05405405]
[0.04826255]
[0.03281853]]] [[0.05984557]]
[[[0.04826255]
[0.03281853]
[0.05984557]]] [[0.08494207]]
[[[0.03281853]
[0.05984557]
[0.08494207]]] [[0.08494207]]
(중략)
[[[0.4131274 ]
[0.52123547]
[0.5965251 ]]] [[0.58108103]]
[[[0.52123547]
[0.5965251 ]
[0.58108103]]] [[0.484556]]
[[[0.5965251 ]
[0.58108103]
[0.484556 ]]] [[0.3899614]]
[[[0.58108103]
[0.484556 ]
[0.3899614 ]]] [[0.3223938]]
[[[0.484556 ]
[0.3899614]
[0.3223938]]] [[0.3899614]]
- Generator가 예쁘게 Train Data를 만들어 주네요.
# Train 완료된 Model로 Predict
pred_generator = TimeseriesGenerator(test, test, length=look_back, batch_size=1)
-
LSTM Input Shape에 Time Steps 값을 넣어줍니다.
-
Generator를 사용할 때는 fit_generator를 사용해 주세요.
# create and fit the LSTM network
model = Sequential()
model.add(LSTM(16, input_shape=(look_back , 1)))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit_generator(train_generator, steps_per_epoch=1, epochs=1000, verbose=2)
Epoch 1/1000
- 1s - loss: 0.0010
Epoch 2/1000
- 0s - loss: 5.6192e-04
Epoch 3/1000
- 0s - loss: 0.0177
Epoch 4/1000
- 0s - loss: 0.0013
Epoch 5/1000
- 0s - loss: 0.0123
Epoch 6/1000
- 0s - loss: 0.0238
Epoch 7/1000
- 0s - loss: 0.0556
Epoch 8/1000
- 0s - loss: 0.0018
Epoch 9/1000
- 0s - loss: 8.9272e-04
Epoch 10/1000
- 0s - loss: 3.9241e-05
(중략)
Epoch 990/1000
- 0s - loss: 0.0035
Epoch 991/1000
- 0s - loss: 0.0106
Epoch 992/1000
- 0s - loss: 5.4522e-05
Epoch 993/1000
- 0s - loss: 0.0016
Epoch 994/1000
- 0s - loss: 0.0088
Epoch 995/1000
- 0s - loss: 0.0087
Epoch 996/1000
- 0s - loss: 0.0015
Epoch 997/1000
- 0s - loss: 0.0023
Epoch 998/1000
- 0s - loss: 6.2472e-04
Epoch 999/1000
- 0s - loss: 8.3021e-04
Epoch 1000/1000
- 0s - loss: 6.5412e-04
import matplotlib.pyplot as plt
hist = model.history
fig, loss_ax = plt.subplots()
acc_ax = loss_ax.twinx()
loss_ax.plot(hist.history['loss'], 'y', label='train loss')
loss_ax.set_xlabel('epoch')
loss_ax.set_ylabel('loss')
loss_ax.legend(loc='upper left')
plt.show()

- Validation Data의 평가결과는 Time Steps를 사용하지 않을 때보다 약간 더 나빠진 것 같습니다.
test_pred = model.predict_generator( pred_generator )
train_pred = model.predict_generator( train_generator )
test_pred = scaler.inverse_transform(test_pred)
train_pred = scaler.inverse_transform(train_pred)
scores = model.evaluate_generator(pred_generator)
print("Look_back : %d - %s: %f" %(look_back, model.metrics_names[0], scores))
Look_back : 3 - loss: 0.018767
trainPredictPlot = np.empty_like(dataset)
trainPredictPlot[:, :] = np.nan
trainPredictPlot[look_back:len(train_pred)+look_back, :] = train_pred
testPredictPlot = np.empty_like(dataset)
testPredictPlot[:, :] = np.nan
testPredictPlot[len(train_pred)+(look_back*2)-1 :len(dataset)-1, :] = test_pred
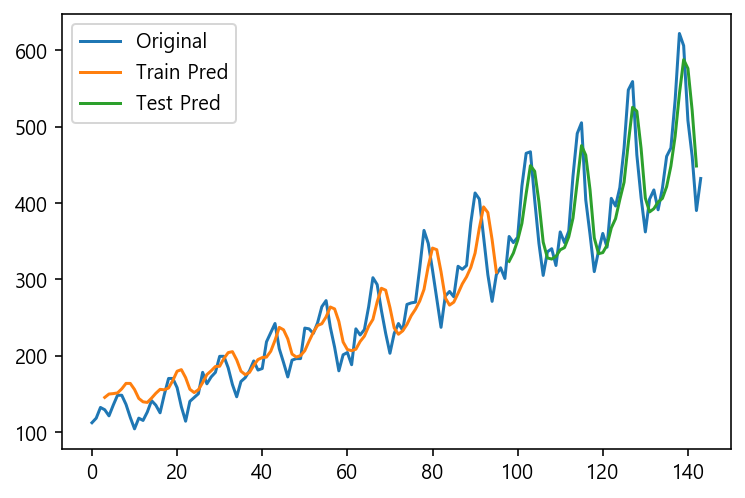
# plot baseline and predictions
plt.plot(scaler.inverse_transform(dataset) , label='Original')
plt.plot(trainPredictPlot , label='Train Pred')
plt.plot(testPredictPlot , label='Test Pred')
plt.legend()
plt.show()
trainY = []
testY = []
for i in range(len(train_generator)):
x, y = train_generator[i]
trainY.append( y[0][0] )
for i in range(len(pred_generator)):
x, y = pred_generator[i]
testY.append( y[0][0] )
trainY = np.reshape(trainY , (len(trainY), 1))
trainY = scaler.inverse_transform( trainY )
# calculate root mean squared error
trainScore = math.sqrt(mean_squared_error(trainY, train_pred))
print('Train Score: %f RMSE' % (trainScore))
testY = np.reshape(testY , (len(testY), 1))
testY = scaler.inverse_transform( testY )
testScore = math.sqrt(mean_squared_error(testY, test_pred))
print('Test Score: %f RMSE' % (testScore))
Train Score: 32.753556 RMSE
Test Score: 70.961880 RMSE
-
RMSE값도 Time Steps를 사용하지 않을때 보다 더 나빠졌네요.
-
뭔가 Hyperparameter를 더 튜닝해야 하는 것일까요?
4. LSTM with Memory Between Batches
-
이번에는 Stateful LSTM을 이용해 보도록 하겠습니다.
-
Data 생성은 이전 방법과 동일하게 Time Steps를 3으로 지정해서 만들어 보겠습니다.
look_back = 3
train_generator = TimeseriesGenerator(train, train, length=look_back, batch_size=1)
len(train_generator)
for i in range(len(train_generator)):
x, y = train_generator[i]
print(x,y)
93
[[[0.01544401]
[0.02702703]
[0.05405405]]] [[0.04826255]]
[[[0.02702703]
[0.05405405]
[0.04826255]]] [[0.03281853]]
[[[0.05405405]
[0.04826255]
[0.03281853]]] [[0.05984557]]
[[[0.04826255]
[0.03281853]
[0.05984557]]] [[0.08494207]]
[[[0.03281853]
[0.05984557]
[0.08494207]]] [[0.08494207]]
(중략)
[[[0.4034749 ]
[0.4131274 ]
[0.52123547]]] [[0.5965251]]
[[[0.4131274 ]
[0.52123547]
[0.5965251 ]]] [[0.58108103]]
[[[0.52123547]
[0.5965251 ]
[0.58108103]]] [[0.484556]]
[[[0.5965251 ]
[0.58108103]
[0.484556 ]]] [[0.3899614]]
[[[0.58108103]
[0.484556 ]
[0.3899614 ]]] [[0.3223938]]
[[[0.484556 ]
[0.3899614]
[0.3223938]]] [[0.3899614]]
# Train 완료된 Model로 Predict
pred_generator = TimeseriesGenerator(test, test, length=look_back, batch_size=1)
- Stateful LSTM에서는 반드시 Batch Size까지 명시적으로 기입한 Input Shape을 입력해 주어야 합니다.
- Stateful LSTM에 관해서는 아래 Link의 Post를 참고해 주시기 바랍니다.
# create and fit the LSTM network
batch_size = 1
model = Sequential()
model.add(LSTM(16, batch_input_shape=(batch_size, look_back, 1), stateful=True))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
for i in range(200):
model.fit_generator(train_generator, verbose=2 , shuffle=False)
model.reset_states()
Epoch 1/1
- 2s - loss: 0.0052
(중략)
Epoch 1/1
- 1s - loss: 0.0014
Epoch 1/1
- 1s - loss: 0.0014
test_pred = model.predict_generator( pred_generator )
train_pred = model.predict_generator( train_generator )
test_pred = scaler.inverse_transform(test_pred)
train_pred = scaler.inverse_transform(train_pred)
scores = model.evaluate_generator(pred_generator)
print("Look_back : %d - %s: %f" %(look_back, model.metrics_names[0], scores))
Look_back : 3 - loss: 0.017854
- Validation Set의 점수는 크게 나아지지 않았습니다.
trainPredictPlot = np.empty_like(dataset)
trainPredictPlot[:, :] = np.nan
trainPredictPlot[look_back:len(train_pred)+look_back, :] = train_pred
testPredictPlot = np.empty_like(dataset)
testPredictPlot[:, :] = np.nan
testPredictPlot[len(train_pred)+(look_back*2)-1 :len(dataset)-1, :] = test_pred
# plot baseline and predictions
plt.plot(scaler.inverse_transform(dataset) , label='Original')
plt.plot(trainPredictPlot , label='Train Pred')
plt.plot(testPredictPlot , label='Test Pred')
plt.legend()
plt.show()

- Train Set에서의 예측은 그럭저럭 하는 것 같은데, Validation Set에서의 그래프는 크게 흔들리는 경향이 있습니다.
trainY = []
testY = []
for i in range(len(train_generator)):
x, y = train_generator[i]
trainY.append( y[0][0] )
for i in range(len(pred_generator)):
x, y = pred_generator[i]
testY.append( y[0][0] )
trainY = np.reshape(trainY , (len(trainY), 1))
trainY = scaler.inverse_transform( trainY )
# calculate root mean squared error
trainScore = math.sqrt(mean_squared_error(trainY, train_pred))
print('Train Score: %f RMSE' % (trainScore))
testY = np.reshape(testY , (len(testY), 1))
testY = scaler.inverse_transform( testY )
testScore = math.sqrt(mean_squared_error(testY, test_pred))
print('Test Score: %f RMSE' % (testScore))
Train Score: 21.649601 RMSE
Test Score: 50.462700 RMSE
- Stateless LSTM보다는 좀 나아졌네요.
5. 비교 Test
- 이번에는 번외로 Timeseriesgenerator를 사용하지 않고 Data Set을 생성해서 Test해보겠습니다.
- 이걸 왜 하냐굽쇼? 혹시나 해서 한 번 해보겠습니다.
import matplotlib.pyplot as plt
import math
import numpy as np
import pandas as pd
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
# fix random seed for reproducibility
np.random.seed(7)
# load the dataset
dataframe = pd.read_csv('airline-passengers.csv', usecols=[1], engine='python')
dataset = dataframe.values
dataset = dataset.astype('float32')
# normalize the dataset
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(dataset)
# split into train and test sets
train_size = int(len(dataset) * 0.67)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
# convert an array of values into a dataset matrix
def create_dataset(dataset, look_back=1):
dataX, dataY = [], []
for i in range(len(dataset)-look_back-1):
a = dataset[i:(i+look_back), 0]
dataX.append(a)
dataY.append(dataset[i + look_back, 0])
return np.array(dataX), np.array(dataY)
# reshape into X=t and Y=t+1
look_back = 1
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)
# reshape input to be [samples, time steps, features]
trainX = np.reshape(trainX, (trainX.shape[0], 1, trainX.shape[1]))
testX = np.reshape(testX, (testX.shape[0], 1, testX.shape[1]))
# create and fit the LSTM network
model = Sequential()
model.add(LSTM(4, input_shape=(1, look_back)))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(trainX, trainY, epochs=100, batch_size=1, verbose=2)
# make predictions
trainPredict = model.predict(trainX)
testPredict = model.predict(testX)
# invert predictions
trainPredict = scaler.inverse_transform(trainPredict)
trainY = scaler.inverse_transform([trainY])
testPredict = scaler.inverse_transform(testPredict)
testY = scaler.inverse_transform([testY])
# calculate root mean squared error
trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:,0]))
print('Test Score: %.2f RMSE' % (testScore))
Epoch 1/100
- 2s - loss: 0.0413
Epoch 2/100
- 1s - loss: 0.0202
Epoch 3/100
- 1s - loss: 0.0146
Epoch 4/100
- 1s - loss: 0.0131
Epoch 5/100
- 1s - loss: 0.0121
Epoch 6/100
- 1s - loss: 0.0111
Epoch 7/100
- 1s - loss: 0.0102
Epoch 8/100
- 1s - loss: 0.0093
Epoch 9/100
- 1s - loss: 0.0081
Epoch 10/100
- 1s - loss: 0.0071
(중략)
Epoch 90/100
- 1s - loss: 0.0020
Epoch 91/100
- 1s - loss: 0.0020
Epoch 92/100
- 1s - loss: 0.0020
Epoch 93/100
- 1s - loss: 0.0021
Epoch 94/100
- 1s - loss: 0.0021
Epoch 95/100
- 1s - loss: 0.0020
Epoch 96/100
- 1s - loss: 0.0020
Epoch 97/100
- 1s - loss: 0.0020
Epoch 98/100
- 1s - loss: 0.0020
Epoch 99/100
- 1s - loss: 0.0020
Epoch 100/100
- 1s - loss: 0.0020
Train Score: 22.92 RMSE
Test Score: 47.53 RMSE
# shift train predictions for plotting
trainPredictPlot = np.empty_like(dataset)
trainPredictPlot[:, :] = np.nan
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict
# shift test predictions for plotting
testPredictPlot = np.empty_like(dataset)
testPredictPlot[:, :] = np.nan
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict
# plot baseline and predictions
plt.plot(scaler.inverse_transform(dataset))
plt.plot(trainPredictPlot)
plt.plot(testPredictPlot)
plt.show()
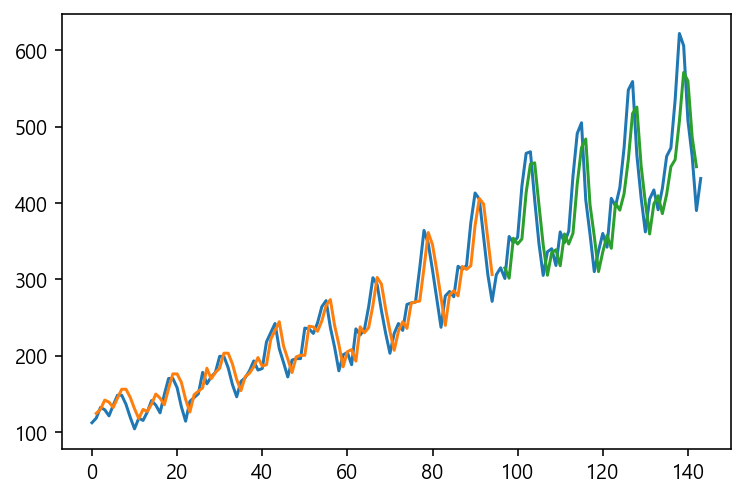
-
흠… 동일한 Input Data Shape을 가지고, 동일한 Network 구조를 가지고 있, 오히려 LSTM Output Neuron의 수는 훨씬 더 적은데도 성능은 상당히 좋습니다.
-
차이점은 TimeseriesGenerator의 사용유무밖에 없는데도 말이죠.
-
혹시 이 차이점을 아시는 분 없을까요?