LSTM Exercise #00 - Alphabet Prediction

LSTM Exercise #00 - Alphabet Prediction

• 앞으로 몇번의 Post를 거쳐서, LSTM을 이용한 다양한 예제들을 다뤄볼 예정입니다.

• LSTM은 Input Data Foramt을 어떻게 구성하느냐에 따라서 성능의 차이도 많이 발생합니다.

• 저는 Data의 Input Format에 따라서 또는 Train 형태에 따라서 Keras LSTM Parameter를 어떻게 구성하고 어떻게 Train 시키는지가 가장 어려웠습니다.

• 매우 다양한 예제가 있고, 다양한 형태로 Input Format을 구성하지만 일목요연하게 설명된 자료를 찾기는 힘들었습니다.

• 제가 여러 예제들을 살펴보면서 다양한 입력 형태들을 확인한 결과를 설명해 보고자 합니다.

Alphabet Prediction

• RNN & LSTM은 다양한 예측 문제에 사용될 수 있습니다. Simple한 예제부터 시작해 보도록 하겠습니다.

• 이번 예제에서 하고자 하는 것은 주어진 하나의 Alphabet 혹은 연속된 Alphabet Sequence 다음에 올 Alphabet을 예측하는 Model을 만드는 것입니다.

0. 준비

• 필요한 Package들을 Load합니다.

• 우리는 Keras & Tensorflow를 사용할 예정입니다.

import numpy
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from keras.utils import np_utils

import matplotlib
from IPython.display import set_matplotlib_formats
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"

%config IPCompleter.greedy=True

from keras.preprocessing.sequence import pad_sequences

• Random Seed를 고정합니다.

numpy.random.seed(7)

• 우리가 학습 및 예측에 사용할 Alphabet 문자입니다.

• Utility 자료구조도 하나 정의합니다.

  • Tensorflow에 Train Data를 입력할 때는 반드시 숫자이어야 합니다.
  • 그러나, Alphabet은 문자이기 때문에 반드시 변환이 필요하며, 문자 <-> 숫자로 상호 변화할 수 있는 Dictionary를 정의합니다.
  • 문자열을 다루는 문제에서는 대부분 이런 자료구조를 이용합니다.

# 학습할 Data
alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"

# 문자 <-> 숫자 상호 변환 Util
char_to_int = dict((c, i) for i, c in enumerate(alphabet))
int_to_char = dict((i, c) for i, c in enumerate(alphabet))

• 사용법은 아래와 같이 사용하시면 됩니다.

char_to_int['C']
int_to_char[7]

2
'H'

• 기본적인 Train Data 생성 함수를 살펴보도록 하겠습니다.

• 아래 함수에서 seq_length 라는 변수가 중요한 변수로 사용됩니다.

• seq_length라는 값은 LSTM이 시계열 Data 혹은 Sequence Data에서 Train시에 과거 몇 개의 Data를 Train에 사용할 것인지를 정하는 아주 아주 중요한 값입니다.

• Time Steps 라는 이름으로도 문서상에서 많이 불려집니다.

• 이 함수가 하는 일을 표현하면 아래와 같습니다.

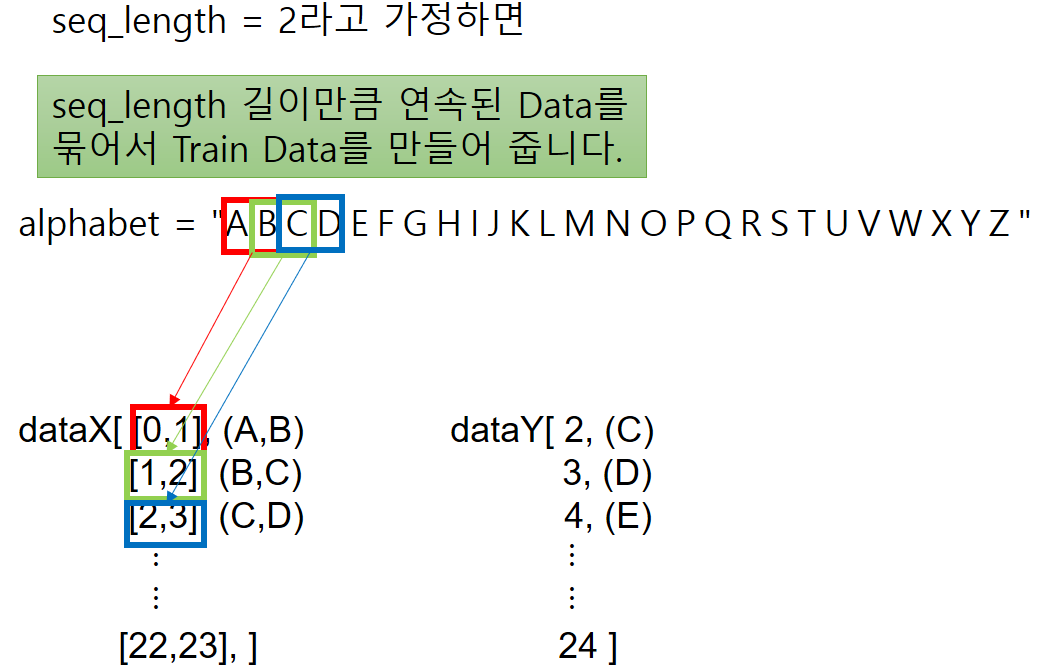
• seq_length 값에 따라서 Train에 사용할 값을 dataX List에 추가하고, 같은 Index에 그에 해당하는 Label(Target)값을 dataY에 저장해 줍니다.
  • dataX : Train Data. 예측할 문자 전에 나오는 문자(열)
  • dataY : Label Data. 예측해야 할 문자

• dataX는 배열의 요소가 배열인 형태로 구성됩니다.

• 실제 Data 출력 Format을 보도록 하겠습니다.

# prepare the dataset of input to output pairs encoded as integers
seq_length = 2
dataX = []
dataY = []

for i in range(0, len(alphabet) - seq_length, 1):
    seq_in = alphabet[i:i + seq_length]
    seq_out = alphabet[i + seq_length]
    dataX.append([char_to_int[char] for char in seq_in])
    dataY.append(char_to_int[seq_out])
    print(seq_in, '->', seq_out)

AB -> C
BC -> D
CD -> E
DE -> F
EF -> G
FG -> H
GH -> I
HI -> J
IJ -> K
JK -> L
KL -> M
LM -> N
MN -> O
NO -> P
OP -> Q
PQ -> R
QR -> S
RS -> T
ST -> U
TU -> V
UV -> W
VW -> X
WX -> Y
XY -> Z

• 실제로 Size와 어떤 Data가 있는지 확인해 보겠습니다.

print("dataX Size : " , len( dataX ) , ",  dataY Size : ", len(dataY) )
print("dataX[0] : ", dataX[0] , "  dataY[0] : " , dataY[0])

dataX Size :  24 ,  dataY Size :  24
dataX[0] :  [0, 1]   dataY[0] :  2

1. LSTM의 Train Data Input Shape

• 제가 LSTM을 공부하면서 가장 혼란스러웠던 부분이 바로 LSTM의 Train Data Input Shape이었습니다.

• 우선 LSTM의 Train Data Input Shape은 반드시 3차원 Array 형태이어야 합니다.

• Keras LSTM API는 input_shape이라는 Parameter를 통해서 Train Data Input Shape을 정합니다.

• 그러나 많은 예제에서 input_shape은 2개의 Parameter만 입력합니다.( 반드시 3차원 Array 형태라고 했는데…? )

• 먼저 input_shape의 2개 Parameter는 각각 순서대로 (time_steps , number_of_features)입니다.

• time_steps는 위에서 알아봤던 내용으로, LSTM에 과거의 Data를 얼마나 많이 입력해 줄 것인가를 정해줍니다.

• number_of_features는 하나의 Data에 얼마나 많은 Feature가 있는지를 정해줍니다.

• 예를 들어 설명해 보겠습니다.

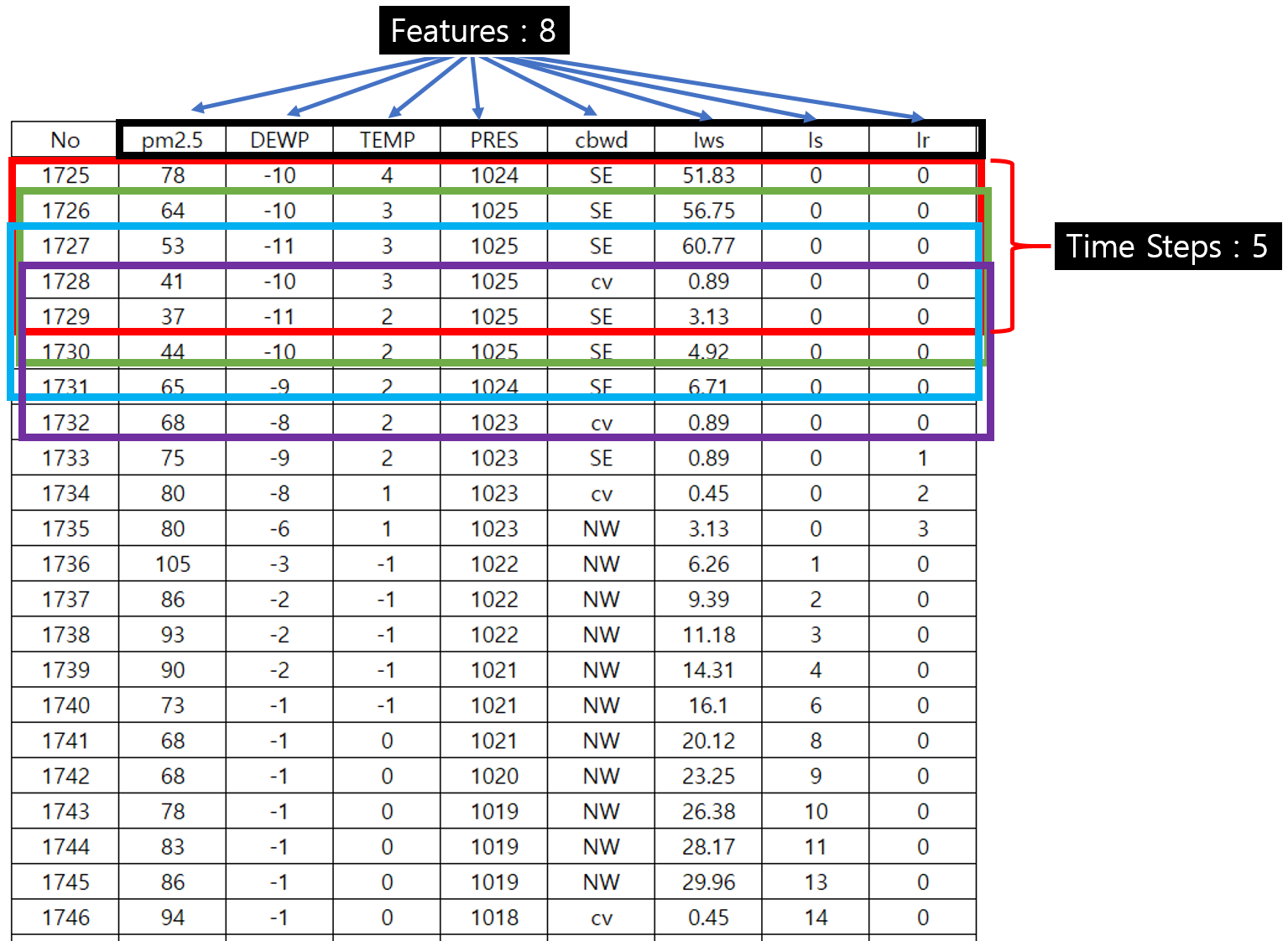
• 위의 그림에서 각 색깔은 하나의 Data로써, time_steps는 5이고, 개별 Data를 이루는 Feature의 수는 8이 됩니다.

• 어떤 Data가 주어지면 Feature의 수는 고정값이 될 것이고, time_steps는 Model의 성능이 가장 좋아지는 적절한 값으로 정해주면 될 것입니다.

• 그리고 언급하지 않은, 혼란을 야기한, 나머지 하나의 값은 number of samples이라는 Parameter로 전체 Data의 개수를 뜻하며 1개 이상이라고 가정합니다.

• 즉, 실제 fit시에 입력으로 들어오는 Train Data의 Shape을 보고 적절한 값이 자동으로 채워지는 것입니다.

• 위에서 설명드린 바와 같이, Input Data Shape을 3차원 Array로 변환합니다.

• 변환은 Numpy Reshape을 쓰시면 됩니다.

# [number_samples, time_steps, features] 순으로 적어줍니다.
# 우리가 다루는 Train Data는 Alhpabet 문자 하나가 Feature이기 때문에 Feature수가 1입니다.
X = numpy.reshape(dataX, (len(dataX), seq_length, 1))

• 만들어진 실제 Data값과 형태를 살펴보도록 하죠

X.shape
X

(24, 2, 1)

array([[[ 0],
        [ 1]],

       [[ 1],
        [ 2]],

       [[ 2],
        [ 3]],

       [[ 3],
        [ 4]],

       [[ 4],
        [ 5]],

       [[ 5],
        [ 6]],

       [[ 6],
        [ 7]],

       [[ 7],
        [ 8]],

       [[ 8],
        [ 9]],

       [[ 9],
        [10]],

       [[10],
        [11]],

       [[11],
        [12]],

       [[12],
        [13]],

       [[13],
        [14]],

       [[14],
        [15]],

       [[15],
        [16]],

       [[16],
        [17]],

       [[17],
        [18]],

       [[18],
        [19]],

       [[19],
        [20]],

       [[20],
        [21]],

       [[21],
        [22]],

       [[22],
        [23]],

       [[23],
        [24]]])

• 실제 Alhpabet 값이 해당하는 숫자로 변환되어 3차원 Array로 저장되어 있는 것을 알 수 있습니다.

• 마지막으로 Normalize 과정을 거칩니다.

• Tree Based Algorithm이 아닌, Neural Net과 같은 Algorithm은 Data를 Normalize해 주어야 좋은 성능이 나옵니다.

# normalize
X = X / float(len(alphabet))
X

array([[[0.        ],
        [0.03846154]],

       [[0.03846154],
        [0.07692308]],

       [[0.07692308],
        [0.11538462]],

       [[0.11538462],
        [0.15384615]],

       [[0.15384615],
        [0.19230769]],

       [[0.19230769],
        [0.23076923]],

       [[0.23076923],
        [0.26923077]],

       [[0.26923077],
        [0.30769231]],

       [[0.30769231],
        [0.34615385]],

       [[0.34615385],
        [0.38461538]],

       [[0.38461538],
        [0.42307692]],

       [[0.42307692],
        [0.46153846]],

       [[0.46153846],
        [0.5       ]],

       [[0.5       ],
        [0.53846154]],

       [[0.53846154],
        [0.57692308]],

       [[0.57692308],
        [0.61538462]],

       [[0.61538462],
        [0.65384615]],

       [[0.65384615],
        [0.69230769]],

       [[0.69230769],
        [0.73076923]],

       [[0.73076923],
        [0.76923077]],

       [[0.76923077],
        [0.80769231]],

       [[0.80769231],
        [0.84615385]],

       [[0.84615385],
        [0.88461538]],

       [[0.88461538],
        [0.92307692]]])

• 이제 Target도 유사한 방식으로 준비를 합니다.

• 다른 점이 있다면, 우리가 예측하려는 것이 26개의 문자(Class)를 분류하는 Categorical Classification 문제이기 때문에 Target값을 One-Hot Encoding을 해준다는 것입니다.

dataY

# one hot encode the output variable
y = np_utils.to_categorical(dataY)

y

[1,
 2,
 3,
 4,
 5,
 6,
 7,
 8,
 9,
 10,
 11,
 12,
 13,
 14,
 15,
 16,
 17,
 18,
 19,
 20,
 21,
 22,
 23,
 24,
 25]


array([[0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        1., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 1., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 1., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 1., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 1., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 1., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 1., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 1., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 1.]], dtype=float32)

• 자, 이제 LSTM을 Train 시킬 기본적인 준비를 마쳤으니, 각 Case별로 알아보도록 하겠습니다.

1. LSTM for Learning One-Char to One-Char Mapping

• 처음으로 다뤄볼 Train 형태는 One-Char To One-Char 예측입니다.

• 쉽게 말하면, 이전의 글자와 다음 글자로 이루어진 Train Set을 학습하고, 특정 글자를 보고 다음 글자를 예측하는 Model입니다.

• 이런 형태의 Classification에 LSTM까지 쓸 필요는 없을 것 같고, Simple한 MLP로도 가능할 것 같습니다만…

• 살펴보도록 하겠습니다.

1.1. Train Data 준비

• 이번 예제는 이전 한 글자(Time Steps = 1)를 보고 다음에 올 한 글자를 예측하는 문제입니다.

• Train Data Set은 한 글자씩 Array로 준비하면 되고, Label(Target)은 다음에 올 한 글자로 준비하면 되겠습니다.

• seq_length(Time Steps)를 1로 하고, Data를 준비하도록 합시다

seq_length = 1
dataX = []
dataY = []

for i in range(0, len(alphabet) - seq_length, 1):
    seq_in = alphabet[i:i + seq_length]
    seq_out = alphabet[i + seq_length]
    dataX.append([char_to_int[char] for char in seq_in])
    dataY.append(char_to_int[seq_out])
    print(seq_in, '->', seq_out)

A -> B
B -> C
C -> D
D -> E
E -> F
F -> G
G -> H
H -> I
I -> J
J -> K
K -> L
L -> M
M -> N
N -> O
O -> P
P -> Q
Q -> R
R -> S
S -> T
T -> U
U -> V
V -> W
W -> X
X -> Y
Y -> Z

• 앞서 말씀드렸듯이, Train Data의 Shape은 3차원 Array이어야 하기 때문에 다음과 같이 Reshape합니다.

• 순서는 (Sample 수 , Time Steps , Feature갯수) 입니다.

• Feature는 문자 하나가 전부이기 때문에 1로 합니다.

X = numpy.reshape(dataX, (len(dataX), seq_length, 1))

• 이후 과정은 기계적으로 반복합니다.

# normalize
X = X / float(len(alphabet))

# one hot encode the output variable
y = np_utils.to_categorical(dataY)

1.2. Build Model & Train

• 이제 중요한 LSTM Network을 구성하는 단계입니다.

• LSTM의 첫번째 Parameter는 units이고, 이는 LSTM의 출력 Neuron 갯수 입니다.

• 너무 적게해도 학습이 되지 않고, 너무 많을 필요도 없으니 Test를 통해 적절한 값을 선택하시면 됩니다.

• 이 문제는 Alphabet 26글자를 분류하는 문제이기 때문에 마지막 Dense 층의 Activation Function으로 Softmax를 붙여줍니다.

• Multiclass Classification 문제이기 때문에 Loss Function은 Categorical Crossentropy를 사용합니다.

• Optimizer는 ADAM을 사용하도록 하죠

• Train Epoch은 500회 반복하도록 하겠습니다.

model = Sequential()
model.add(LSTM(32, input_shape=(X.shape[1], X.shape[2])))
model.add(Dense(y.shape[1], activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X, y, epochs=500, batch_size=1, verbose=2)

Epoch 1/500
 - 4s - loss: 3.2677 - acc: 0.0400
Epoch 2/500
 - 0s - loss: 3.2596 - acc: 0.0000e+00
Epoch 3/500
 - 0s - loss: 3.2566 - acc: 0.0400
Epoch 4/500
 - 0s - loss: 3.2540 - acc: 0.0400
Epoch 5/500
 - 0s - loss: 3.2511 - acc: 0.0400
Epoch 6/500
 - 0s - loss: 3.2481 - acc: 0.0400
Epoch 7/500
 - 0s - loss: 3.2451 - acc: 0.0400
Epoch 8/500
 - 0s - loss: 3.2421 - acc: 0.0000e+00
Epoch 9/500
 - 0s - loss: 3.2393 - acc: 0.0400
Epoch 10/500
 - 0s - loss: 3.2359 - acc: 0.0400
 
 (중략)
 
 Epoch 490/500
 - 0s - loss: 1.7083 - acc: 0.8000
Epoch 491/500
 - 0s - loss: 1.7077 - acc: 0.8000
Epoch 492/500
 - 0s - loss: 1.7062 - acc: 0.8000
Epoch 493/500
 - 0s - loss: 1.7073 - acc: 0.7600
Epoch 494/500
 - 0s - loss: 1.7062 - acc: 0.8000
Epoch 495/500
 - 0s - loss: 1.7072 - acc: 0.7600
Epoch 496/500
 - 0s - loss: 1.7039 - acc: 0.7600
Epoch 497/500
 - 0s - loss: 1.7035 - acc: 0.8000
Epoch 498/500
 - 0s - loss: 1.7023 - acc: 0.8000
Epoch 499/500
 - 0s - loss: 1.6979 - acc: 0.8000
Epoch 500/500
 - 0s - loss: 1.6993 - acc: 0.8000
 
 <keras.callbacks.History at 0x12dff9f5788>

1.3. Summarize Performance of Model

scores = model.evaluate(X, y, verbose=0)
print("Model Accuracy: %.2f%%" % (scores[1]*100))

Model Accuracy: 84.00%

• 열심히 Train을 마치고 결과를 살펴보니 Accuracy가 84% 정도 나오네요.

• 나쁘다고도 할 순 없지만, 썩 좋지도 않습니다.

• 다른 사람들도 Train 마치고 Loss과 Accuracy 그래프 그리길래 저도 한 번 그려봤습니다.

hist = model.history

import matplotlib.pyplot as plt

fig, loss_ax = plt.subplots()
acc_ax = loss_ax.twinx()

loss_ax.plot(hist.history['loss'], 'y', label='train loss')
loss_ax.set_xlabel('epoch')
loss_ax.set_ylabel('loss')
loss_ax.legend(loc='upper left')

acc_ax.plot(hist.history['acc'], 'b', label='train acc')
acc_ax.set_ylabel('accuracy')
acc_ax.legend(loc='upper left')

plt.show()

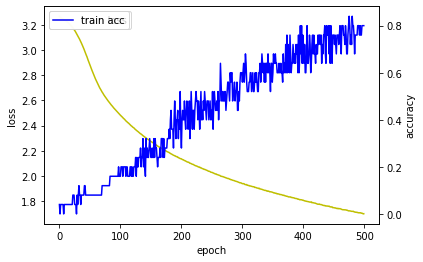
• 훈련한 Model을 이용해서 예측을 잘 하는지 한 번 살펴보도록 하겠습니다.

• Alphabet을 처음부터 다 한 번씩 넣어보면서 다음 글자를 잘 예측하는지 보는 것입니다.

• 염두해 둘 점은 Train된 Model을 이용하여 Predict할 때는 Train할 때 이용한 Train Data와 동일한 Shape으로 입력해 주어야 합니다.

# demonstrate some model predictions
for pattern in dataX:
    x = numpy.reshape(pattern, (1, len(pattern), 1))
    x = x / float(len(alphabet))
    prediction = model.predict(x, verbose=0)
    index = numpy.argmax(prediction)
    result = int_to_char[index]
    seq_in = [int_to_char[value] for value in pattern]
    print(seq_in, "->", result)

['A'] -> B
['B'] -> B
['C'] -> D
['D'] -> E
['E'] -> F
['F'] -> G
['G'] -> H
['H'] -> I
['I'] -> J
['J'] -> K
['K'] -> L
['L'] -> M
['M'] -> N
['N'] -> O
['O'] -> P
['P'] -> Q
['Q'] -> R
['R'] -> S
['S'] -> T
['T'] -> U
['U'] -> V
['V'] -> Y
['W'] -> Y
['X'] -> Z
['Y'] -> Z

• 군데군데 틀린 곳이 보이네요. 흠… 역시 84%

• 사실 이런 Network 구조는 LSTM의 능력을 십분발휘하기에 좋은 구조는 아닙니다.

• 각각의 Input-Output Data는 연관성이 없이 Random하고, 학습마다 Network 상태는 Reset됩니다.(Batch 마다 Reset되지만, 이 예제에서 Batch Size는 1입니다.)

• LSTM이 잘하는 것은 과거일을 기억하여 미래를 예측하는 것입니다.

• LSTM이 좀 더 잘 할 수 있도록 Train Data Shape을 조절해 보겠습니다.

2. LSTM for a Feature Window to One-Char Mapping

• 이번에는 Window Method라는 방법을 사용해 보도록 하겠습니다.

• Network에 주입하는 Data Shape에서 Feature 개수를 이전의 1개에서 3개로 늘리는 것입니다.

• Feature가 많을수록 예측려이 높아질 것으로 예상됩니다.

• 다음 예제에서 혼돈스러울 수도 있는데, seq_length를 앞에서 Time Steps와 동일한 개념으로 설명드렸는데, 이번 예제에는 Feature 개수와 동일한 개념으로 사용하고 있습니다.

• 즉, 과거 3개의 Data를 보겠다는 것이 아니고, 과거 1개의 Data만 살피지만 Feature가 3개인 Data를 사용해서 Train하겠다는 의미입니다.

2.1. Prepare Train Data

• Feature 수를 3개로 늘린 Data를 준비하도록 하겠습니다.

seq_length = 3

dataX = []
dataY = []

for i in range(0, len(alphabet) - seq_length, 1):
    seq_in = alphabet[i:i + seq_length]
    seq_out = alphabet[i + seq_length]
    dataX.append([char_to_int[char] for char in seq_in])
    dataY.append(char_to_int[seq_out])
    print(seq_in, '->', seq_out)

ABC -> D
BCD -> E
CDE -> F
DEF -> G
EFG -> H
FGH -> I
GHI -> J
HIJ -> K
IJK -> L
JKL -> M
KLM -> N
LMN -> O
MNO -> P
NOP -> Q
OPQ -> R
PQR -> S
QRS -> T
RST -> U
STU -> V
TUV -> W
UVW -> X
VWX -> Y
WXY -> Z

• 보시다시피 각 Dataset의 Featur가 3개가 되고, Target은 그 다음에 올 문자가 된 Train Data가 준비되었습니다.

• 앞서 말씀드렸듯이, LSTM의 Input Shape은 3차원 Array이어야 합니다.

• 우리가 하려는 목적에 맞게 Reshape합니다.

• 주의할 점은 Time Steps은 1이고, Feature가 3개입니다.

# [samples, time steps, features]
X = numpy.reshape(dataX, (len(dataX), 1, seq_length))

X.shape
X

(23, 1, 3)

array([[[ 0,  1,  2]],
       [[ 1,  2,  3]],    
       [[ 2,  3,  4]],    
       [[ 3,  4,  5]],    
       [[ 4,  5,  6]],    
       [[ 5,  6,  7]],    
       [[ 6,  7,  8]],    
       [[ 7,  8,  9]],    
       [[ 8,  9, 10]],    
       [[ 9, 10, 11]],    
       [[10, 11, 12]],    
       [[11, 12, 13]],    
       [[12, 13, 14]],    
       [[13, 14, 15]],    
       [[14, 15, 16]],    
       [[15, 16, 17]],    
       [[16, 17, 18]],    
       [[17, 18, 19]],    
       [[18, 19, 20]],    
       [[19, 20, 21]],    
       [[20, 21, 22]],    
       [[21, 22, 23]],    
       [[22, 23, 24]]])

# normalize
X = X / float(len(alphabet))
X

array([[[0.        , 0.03846154, 0.07692308]],    
       [[0.03846154, 0.07692308, 0.11538462]],    
       [[0.07692308, 0.11538462, 0.15384615]],    
       [[0.11538462, 0.15384615, 0.19230769]],    
       [[0.15384615, 0.19230769, 0.23076923]],    
       [[0.19230769, 0.23076923, 0.26923077]],    
       [[0.23076923, 0.26923077, 0.30769231]],    
       [[0.26923077, 0.30769231, 0.34615385]],    
       [[0.30769231, 0.34615385, 0.38461538]],    
       [[0.34615385, 0.38461538, 0.42307692]],    
       [[0.38461538, 0.42307692, 0.46153846]],    
       [[0.42307692, 0.46153846, 0.5       ]],    
       [[0.46153846, 0.5       , 0.53846154]],    
       [[0.5       , 0.53846154, 0.57692308]],    
       [[0.53846154, 0.57692308, 0.61538462]],    
       [[0.57692308, 0.61538462, 0.65384615]],    
       [[0.61538462, 0.65384615, 0.69230769]],    
       [[0.65384615, 0.69230769, 0.73076923]],    
       [[0.69230769, 0.73076923, 0.76923077]],    
       [[0.73076923, 0.76923077, 0.80769231]],    
       [[0.76923077, 0.80769231, 0.84615385]],    
       [[0.80769231, 0.84615385, 0.88461538]],    
       [[0.84615385, 0.88461538, 0.92307692]]])

# one hot encode the output variable
y = np_utils.to_categorical(dataY)

2.2. Build Model & Train

• Model의 구조는 이전 Model과 동일합니다.

# create and fit the model
model = Sequential()
model.add(LSTM(32, input_shape=(X.shape[1], X.shape[2])))
model.add(Dense(y.shape[1], activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X, y, epochs=500, batch_size=1, verbose=2)

Epoch 1/500
 - 3s - loss: 3.2629 - acc: 0.0000e+00
Epoch 2/500
 - 0s - loss: 3.2515 - acc: 0.0435
Epoch 3/500
 - 0s - loss: 3.2458 - acc: 0.0435
Epoch 4/500
 - 0s - loss: 3.2396 - acc: 0.0000e+00
Epoch 5/500
 - 0s - loss: 3.2332 - acc: 0.0000e+00
Epoch 6/500
 - 0s - loss: 3.2261 - acc: 0.0000e+00
Epoch 7/500
 - 0s - loss: 3.2193 - acc: 0.0435
Epoch 8/500
 - 0s - loss: 3.2118 - acc: 0.0435
Epoch 9/500
 - 0s - loss: 3.2043 - acc: 0.0000e+00
Epoch 10/500
 - 0s - loss: 3.1954 - acc: 0.0435
 
 (중략)
 
 Epoch 490/500
 - 0s - loss: 1.6080 - acc: 0.8261
Epoch 491/500
 - 0s - loss: 1.6089 - acc: 0.7826
Epoch 492/500
 - 0s - loss: 1.6090 - acc: 0.8261
Epoch 493/500
 - 0s - loss: 1.6055 - acc: 0.8696
Epoch 494/500
 - 0s - loss: 1.6047 - acc: 0.8261
Epoch 495/500
 - 0s - loss: 1.6057 - acc: 0.7826
Epoch 496/500
 - 0s - loss: 1.6028 - acc: 0.8261
Epoch 497/500
 - 0s - loss: 1.6055 - acc: 0.8261
Epoch 498/500
 - 0s - loss: 1.6016 - acc: 0.8261
Epoch 499/500
 - 0s - loss: 1.6015 - acc: 0.8261
Epoch 500/500
 - 0s - loss: 1.6001 - acc: 0.7826

hist = model.history

import matplotlib.pyplot as plt

fig, loss_ax = plt.subplots()
acc_ax = loss_ax.twinx()

loss_ax.plot(hist.history['loss'], 'y', label='train loss')
loss_ax.set_xlabel('epoch')
loss_ax.set_ylabel('loss')
loss_ax.legend(loc='upper left')

acc_ax.plot(hist.history['acc'], 'b', label='train acc')
acc_ax.set_ylabel('accuracy')
acc_ax.legend(loc='upper left')

plt.show()

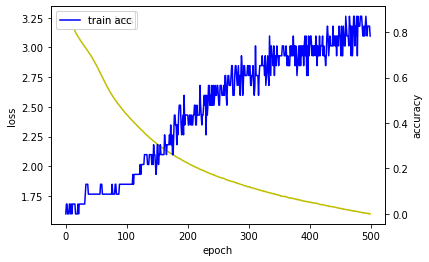
2.3. Summarize Performance of Model

scores = model.evaluate(X, y, verbose=0)
print("Model Accuracy: %.2f%%" % (scores[1]*100))

# demonstrate some model predictions
for pattern in dataX:
    x = numpy.reshape(pattern, (1, 1, len(pattern)))
    x = x / float(len(alphabet))
    prediction = model.predict(x, verbose=0)
    index = numpy.argmax(prediction)
    result = int_to_char[index]
    seq_in = [int_to_char[value] for value in pattern]
    print(seq_in, "->", result)

Model Accuracy: 86.96%
['A', 'B', 'C'] -> D
['B', 'C', 'D'] -> E
['C', 'D', 'E'] -> F
['D', 'E', 'F'] -> G
['E', 'F', 'G'] -> H
['F', 'G', 'H'] -> I
['G', 'H', 'I'] -> J
['H', 'I', 'J'] -> K
['I', 'J', 'K'] -> L
['J', 'K', 'L'] -> M
['K', 'L', 'M'] -> N
['L', 'M', 'N'] -> O
['M', 'N', 'O'] -> P
['N', 'O', 'P'] -> Q
['O', 'P', 'Q'] -> R
['P', 'Q', 'R'] -> S
['Q', 'R', 'S'] -> T
['R', 'S', 'T'] -> U
['S', 'T', 'U'] -> V
['T', 'U', 'V'] -> X
['U', 'V', 'W'] -> Z
['V', 'W', 'X'] -> Z
['W', 'X', 'Y'] -> Z

• 이전 방법보다 좀 더 나아진 것 같아보이지만, Train 할 때 마다 Accuracy가 달라지기 때문에 확실히 더 낫다고 할 수는 없을 것 같습니다.

• 사실 이렇게 LSTM을 이용하는 것은 LSTM의 진정한 능력을 발휘하는 것이 아닙니다.

• LSTM을 좀 더 잘 이용하려면, 위와 같이 하나의 Train Data에 3개의 Feature를 사용하는 것보다 Feature가 하나더라도 Time Steps을 이용하는 것이 훨씬 더 LSTM Network가 학습하기 좋습니다.

• 지금까지의 예제에서는 Time Steps를 1로 했지만, 다음 예제에서는 Time Steps를 이용해 보도록 하겠습니다.

3. LSTM for a Time Step Window to One-Char Mapping

• Keras의 LSTM을 구현할 때는 앞서 살펴본 바와 같이 하나의 Time Steps에 여러개의 Feature를 넣는 것 보다, Time Steps를 여러개 주는 것을 더 좋다고 합니다.

• 이번에는 Time Steps를 이용해 보도록 하겠습니다.

3.1. Prepare Train Data

• Data 준비는 앞의 예제와 동일합니다.

seq_length = 3
dataX = []
dataY = []

for i in range(0, len(alphabet) - seq_length, 1):
    seq_in = alphabet[i:i + seq_length]
    seq_out = alphabet[i + seq_length]
    dataX.append([char_to_int[char] for char in seq_in])
    dataY.append(char_to_int[seq_out])
    print(seq_in, '->', seq_out)

ABC -> D
BCD -> E
CDE -> F
DEF -> G
EFG -> H
FGH -> I
GHI -> J
HIJ -> K
IJK -> L
JKL -> M
KLM -> N
LMN -> O
MNO -> P
NOP -> Q
OPQ -> R
PQR -> S
QRS -> T
RST -> U
STU -> V
TUV -> W
UVW -> X
VWX -> Y
WXY -> Z

• 이번에는 Time Steps를 3으로 하고, Feature를 1로 만든 Shape으로 Data를 Reshape하도록 하겠습니다.

• 앞에서의 예제에서는 Data Shape이 (23 , 1, 3)이었습니다만, 이번에는 (23,3,1)의 Shape이 되도록 만들겠습니다.

• 즉, 다음 문자를 예측하는 Model을 Train할 때, 이전 문자 3개를 보고 다음 문자를 예측하도록 Train시키는 것입니다.

• (A,B,C)가 순서대로 올 때 다음 문자는 D이다 라는 Data Set을 만들어 Train 시킨다는 의미입니다.

• 앞의 예제의 Data Shape과의 차이가 애매하긴 합니다만, 성능의 차이는 큽니다.

# reshape X to be [samples, time steps, features]
X = numpy.reshape(dataX, (len(dataX), seq_length, 1))
X.shape
X

(23, 3, 1)

array([[[ 0],
        [ 1],
        [ 2]],

       [[ 1],
        [ 2],
        [ 3]],

       [[ 2],
        [ 3],
        [ 4]],

       [[ 3],
        [ 4],
        [ 5]],

       [[ 4],
        [ 5],
        [ 6]],

       [[ 5],
        [ 6],
        [ 7]],

       [[ 6],
        [ 7],
        [ 8]],

       [[ 7],
        [ 8],
        [ 9]],

       [[ 8],
        [ 9],
        [10]],

       [[ 9],
        [10],
        [11]],

       [[10],
        [11],
        [12]],

       [[11],
        [12],
        [13]],

       [[12],
        [13],
        [14]],

       [[13],
        [14],
        [15]],

       [[14],
        [15],
        [16]],

       [[15],
        [16],
        [17]],

       [[16],
        [17],
        [18]],

       [[17],
        [18],
        [19]],

       [[18],
        [19],
        [20]],

       [[19],
        [20],
        [21]],

       [[20],
        [21],
        [22]],

       [[21],
        [22],
        [23]],

       [[22],
        [23],
        [24]]])

# normalize
X = X / float(len(alphabet))

# one hot encode the output variable
y = np_utils.to_categorical(dataY)

3.2. Build Model & Train

• Model의 구조는 이전 Model과 동일합니다.

# create and fit the model
model = Sequential()
model.add(LSTM(32, input_shape=(X.shape[1], X.shape[2])))
model.add(Dense(y.shape[1], activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X, y, epochs=500, batch_size=1, verbose=2)

Epoch 1/500
 - 1s - loss: 3.2672 - acc: 0.0000e+00
Epoch 2/500
 - 0s - loss: 3.2536 - acc: 0.0435
Epoch 3/500
 - 0s - loss: 3.2455 - acc: 0.0435
Epoch 4/500
 - 0s - loss: 3.2385 - acc: 0.0435
Epoch 5/500
 - 0s - loss: 3.2314 - acc: 0.0435
Epoch 6/500
 - 0s - loss: 3.2226 - acc: 0.0435
Epoch 7/500
 - 0s - loss: 3.2143 - acc: 0.0435
Epoch 8/500
 - 0s - loss: 3.2047 - acc: 0.0435
Epoch 9/500
 - 0s - loss: 3.1951 - acc: 0.0435
Epoch 10/500
 - 0s - loss: 3.1833 - acc: 0.0435
 
 (중략)
 
 Epoch 490/500
 - 0s - loss: 0.2492 - acc: 1.0000
Epoch 491/500
 - 0s - loss: 0.2490 - acc: 0.9565
Epoch 492/500
 - 0s - loss: 0.2520 - acc: 1.0000
Epoch 493/500
 - 0s - loss: 0.2530 - acc: 1.0000
Epoch 494/500
 - 0s - loss: 0.2530 - acc: 0.9565
Epoch 495/500
 - 0s - loss: 0.2473 - acc: 1.0000
Epoch 496/500
 - 0s - loss: 0.2504 - acc: 1.0000
Epoch 497/500
 - 0s - loss: 0.2463 - acc: 1.0000
Epoch 498/500
 - 0s - loss: 0.2444 - acc: 1.0000
Epoch 499/500
 - 0s - loss: 0.2457 - acc: 1.0000
Epoch 500/500
 - 0s - loss: 0.2474 - acc: 1.0000

hist = model.history

import matplotlib.pyplot as plt

fig, loss_ax = plt.subplots()
acc_ax = loss_ax.twinx()

loss_ax.plot(hist.history['loss'], 'y', label='train loss')
loss_ax.set_xlabel('epoch')
loss_ax.set_ylabel('loss')
loss_ax.legend(loc='upper left')

acc_ax.plot(hist.history['acc'], 'b', label='train acc')
acc_ax.set_ylabel('accuracy')
acc_ax.legend(loc='upper left')

plt.show()

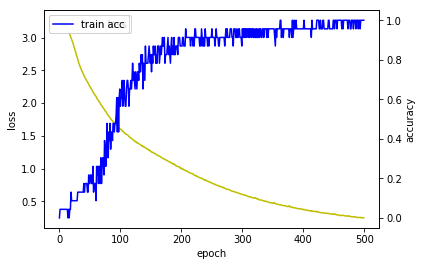
3.3. Summarize Performance of Model

# summarize performance of the model
scores = model.evaluate(X, y, verbose=0)
print("Model Accuracy: %.2f%%" % (scores[1]*100))

Model Accuracy: 100.00%

• 와우..! 100% 정확도라니~!

• Train Data Shape 하나 바꿨을 뿐인데, 성능차이는 확실합니다.

• 확일해 볼까요

• 다시 한 번 말씀드리지만, Predict할 때 Data Shape은 반드시 Train 시킬 때의 Data Shape과 동일해야 합니다.

• 즉, (1,3,1)이 되어야 합니다.

# demonstrate some model predictions
for pattern in dataX:
    x = numpy.reshape(pattern, (1, len(pattern), 1))    
    x = x / float(len(alphabet))        
    prediction = model.predict(x, verbose=0)
    index = numpy.argmax(prediction)
    result = int_to_char[index]
    seq_in = [int_to_char[value] for value in pattern]
    print(seq_in, "->", result)

['A', 'B', 'C'] -> D
['B', 'C', 'D'] -> E
['C', 'D', 'E'] -> F
['D', 'E', 'F'] -> G
['E', 'F', 'G'] -> H
['F', 'G', 'H'] -> I
['G', 'H', 'I'] -> J
['H', 'I', 'J'] -> K
['I', 'J', 'K'] -> L
['J', 'K', 'L'] -> M
['K', 'L', 'M'] -> N
['L', 'M', 'N'] -> O
['M', 'N', 'O'] -> P
['N', 'O', 'P'] -> Q
['O', 'P', 'Q'] -> R
['P', 'Q', 'R'] -> S
['Q', 'R', 'S'] -> T
['R', 'S', 'T'] -> U
['S', 'T', 'U'] -> V
['T', 'U', 'V'] -> W
['U', 'V', 'W'] -> X
['V', 'W', 'X'] -> Y
['W', 'X', 'Y'] -> Z

• 아주 예측을 잘 하네요. 지금까지 본 결과중에 가장 좋네요.

• 입력 Data Shape을 바꿔서 LSTM의 특성과 장점을 살려서 Train 시킨 결과입니다.

• 굳이 이 Model의 단점을 하나 꼽으라면, 하나의 문자를 예측하기 위해서 과거 3개의 문자를 입력으로 넣어주어야 한다는 것입니다.

• LSTM Network의 가장 큰 특징이자 장점 중의 하나가 LSTM Network은 Stateful하다는 것입니다.

• Network이 ‘Stateful하다’라는 것은 Batch 내에서 Network State가 유지된다는 것입니다.
  ( Keras의 Stateful LSTM에 관해서는 추후에 좀 더 자세히 다루도록 하겠습니다. )

• 하지만, Batch Size만큼 학습을 마치면, Network이 Reset되어 다음 학습에서는 사용하지 못합니다.

• 앞의 예제들은 모두 Batch Size를 1로 주었습니다. 즉, 개별 Data Set의 학습이 다른 Data Set의 학습에 도움을 주지 못합니다.

• 다음 예제에서는 하나의 Train시에 전체 Data를 모두 넣어서 전체 Sequence를 다 학습할 수 있도록 Train해 보도록 하겠습니다.

4. LSTM State Maintained Between Samples Within A Batch

• LSTM의 Default 설정은 Batch내에서 State를 유지하고, Batch Train이 끝나면 State를 Reset해버립니다.

• 이번에 알아볼 방법은 전체 학습 동안 State를 유지하기 위해서 Batch Size를 전체 Train Data를 모두 포함할 수 있도록 하는 방법입니다.

• 방법은 Simple합니다. Batch Size를 Sample 전체 갯수로 설정해주면 됩니다.

• 이렇게 하면 LSTM은 Alphabet 전체 순서를 학습할 것입니다.

• 주의할 점은 Keras LSTM은 Data를 섞어버리기(Shuflle) 때문에 Train시에 shuffle option을 Disable해주어야 합니다.

# prepare the dataset of input to output pairs encoded as integers
seq_length = 1
dataX = []
dataY = []

for i in range(0, len(alphabet) - seq_length, 1):
    seq_in = alphabet[i:i + seq_length]
    seq_out = alphabet[i + seq_length]
    dataX.append([char_to_int[char] for char in seq_in])
    dataY.append(char_to_int[seq_out])
    print(seq_in, '->', seq_out)

A -> B
B -> C
C -> D
D -> E
E -> F
F -> G
G -> H
H -> I
I -> J
J -> K
K -> L
L -> M
M -> N
N -> O
O -> P
P -> Q
Q -> R
R -> S
S -> T
T -> U
U -> V
V -> W
W -> X
X -> Y
Y -> Z

# convert list of lists to array and pad sequences if needed
X = pad_sequences(dataX, maxlen=seq_length, dtype='float32')

X = numpy.reshape(dataX, (X.shape[0], seq_length, 1))
X.shape

(25, 1, 1)

# normalize
X = X / float(len(alphabet))

# one hot encode the output variable
y = np_utils.to_categorical(dataY)

• Train할 때 Batch Size를 Data Sample 전체 Size로 설정해 줍니다.

# create and fit the model
model = Sequential()
model.add(LSTM(16, input_shape=(X.shape[1], X.shape[2])))
model.add(Dense(y.shape[1], activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X, y, epochs=5000, batch_size=len(dataX), verbose=2, shuffle=False)

Epoch 1/5000    
 - 4s - loss: 3.2569 - acc: 0.0400
Epoch 2/5000
 - 0s - loss: 3.2566 - acc: 0.0400
Epoch 3/5000
 - 0s - loss: 3.2564 - acc: 0.0400
Epoch 4/5000
 - 0s - loss: 3.2561 - acc: 0.0400
Epoch 5/5000
 - 0s - loss: 3.2558 - acc: 0.0400
Epoch 6/5000
 - 0s - loss: 3.2555 - acc: 0.0400
Epoch 7/5000
 - 0s - loss: 3.2552 - acc: 0.0400
Epoch 8/5000
 - 0s - loss: 3.2549 - acc: 0.0400
Epoch 9/5000
 - 0s - loss: 3.2547 - acc: 0.0400
Epoch 10/5000
 - 0s - loss: 3.2544 - acc: 0.0400
 
 (중략)
 
 Epoch 4990/5000
 - 0s - loss: 0.9022 - acc: 1.0000
Epoch 4991/5000
 - 0s - loss: 0.9020 - acc: 1.0000
Epoch 4992/5000
 - 0s - loss: 0.9018 - acc: 1.0000
Epoch 4993/5000
 - 0s - loss: 0.9017 - acc: 1.0000
Epoch 4994/5000
 - 0s - loss: 0.9015 - acc: 1.0000
Epoch 4995/5000
 - 0s - loss: 0.9013 - acc: 1.0000
Epoch 4996/5000
 - 0s - loss: 0.9011 - acc: 1.0000
Epoch 4997/5000
 - 0s - loss: 0.9010 - acc: 1.0000
Epoch 4998/5000
 - 0s - loss: 0.9008 - acc: 1.0000
Epoch 4999/5000
 - 0s - loss: 0.9006 - acc: 1.0000
Epoch 5000/5000
 - 0s - loss: 0.9004 - acc: 1.0000

hist = model.history

import matplotlib.pyplot as plt

fig, loss_ax = plt.subplots()
acc_ax = loss_ax.twinx()

loss_ax.plot(hist.history['loss'], 'y', label='train loss')
loss_ax.set_xlabel('epoch')
loss_ax.set_ylabel('loss')
loss_ax.legend(loc='upper left')

acc_ax.plot(hist.history['acc'], 'b', label='train acc')
acc_ax.set_ylabel('accuracy')
acc_ax.legend(loc='upper left')

plt.show()

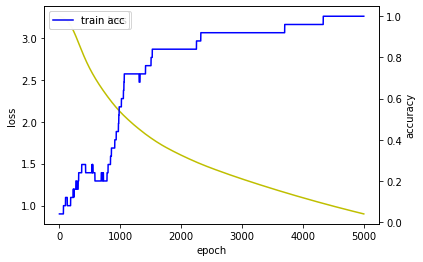
# summarize performance of the model
scores = model.evaluate(X, y, verbose=0)
print("Model Accuracy: %.2f%%" % (scores[1]*100))

Model Accuracy: 100.00%

# demonstrate some model predictions
for pattern in dataX:
    x = numpy.reshape(pattern, (1, len(pattern), 1))
    x = x / float(len(alphabet))
    prediction = model.predict(x, verbose=0)
    index = numpy.argmax(prediction)
    result = int_to_char[index]
    seq_in = [int_to_char[value] for value in pattern]
    print(seq_in, "->", result)

['A'] -> B
['B'] -> C
['C'] -> D
['D'] -> E
['E'] -> F
['F'] -> G
['G'] -> H
['H'] -> I
['I'] -> J
['J'] -> K
['K'] -> L
['L'] -> M
['M'] -> N
['N'] -> O
['O'] -> P
['P'] -> Q
['Q'] -> R
['R'] -> S
['S'] -> T
['T'] -> U
['U'] -> V
['V'] -> W
['W'] -> X
['X'] -> Y
['Y'] -> Z

# demonstrate predicting random patterns
print("Test a Random Pattern:")

for i in range(0,20):
    pattern_index = numpy.random.randint(len(dataX))
    pattern = dataX[pattern_index]
    x = numpy.reshape(pattern, (1, len(pattern), 1))
    x = x / float(len(alphabet))
    prediction = model.predict(x, verbose=0)
    index = numpy.argmax(prediction)
    result = int_to_char[index]
    seq_in = [int_to_char[value] for value in pattern]
    print(seq_in, "->", result)

Test a Random Pattern:
['K'] -> L
['A'] -> B
['N'] -> O
['S'] -> T
['G'] -> H
['K'] -> L
['T'] -> U
['X'] -> Y
['G'] -> H
['Q'] -> R
['X'] -> Y
['I'] -> J
['N'] -> O
['U'] -> V
['H'] -> I
['S'] -> T
['I'] -> J
['R'] -> S
['C'] -> D
['A'] -> B

• 예상대로 LSTM은 전체 Sample에 대해서 학습을 잘 진행하였고, 게다가 Random한 문자예측도 정확하게 수행합니다.

5. Stateful LSTM for a One-Char to One-Char Mapping

• 우선 Stateful LSTM이 무엇인지 부터 알아보도록 하겠습니다.
• http://philipperemy.github.io/keras-stateful-lstm/

5.1. Stateful LSTM

• LSTM에서 Stateful은 Batch내에서 Network의 상태가 다음 Batch Train의 시작에서 그대로 사용된다는 의미입니다.

• 많은 사람들이 Stateful LSTM에 대해서 오해를 하는 경우가 많습니다.

• 이것이 정확히 무엇을 의미하는지 좀 더 자세히 알아보도록 하겠습니다.

• RNN에서 Vanishing Gradient 문제에 직면하게 됩니다.

• RNN뿐 아니라, Vanishing Gradient 문제는 기울기를 이용한 학습 방법과 Backpropagation을 사용한 Artificial Neural Network을 훈련시키는 데 늘 문제가 되었습니다.

• Neural Network은 Train시에 반복해서 Weight를 기울기에 비례하여 Update하는데, tanh같은 기존의 Activation Function은 출력이 (-1 ~ 1) 혹은 (0,1)의 범위를 가지고 있어서 Layer가 거듭될수록(즉, Train이 진행될수록 )Error Signal이 매우 작아지게 된다.

• **이 문제를 개선하기 위한 한 가지 해결책은 Weight를 Update할 때 곱하는 대신 더하는 것입니다. **

• LSTM은 이 방식을 채택하고 있습니다. ( 아래 수식 9번 )

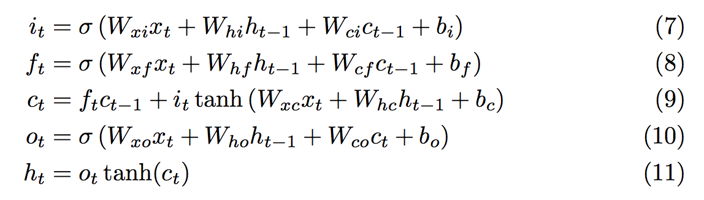
• 이런 설명은 Stateful에 대해서 충분한 설명이 되지 못하는 것 같아 Q&A를 통해서 예제 중심으로 살펴보도록 하겠습니다.

• Q : 큰 Sequence (Ex : Time Series)가 주어지고 Train Input Data X를 만들기 위해 작은 Sequence(Batch)로 나눌 경우에, LSTM은 이 Batch들 사이의 Dependency를 찾을 수 있습니까?

• A : Stateful LSTM은 가능하지만, Stateless LSTM은 할 수 없습니다.

  Stateless LSTM이 대부분의 문제를 해결할 수 있기 때문에 Stateful LSTM을 사용하고자 한다면 실제로 해당 문제를 해결하는데 Stateful LSTM이 진짜 필요한지 생각해 볼 필요가 있습니다.

  Stateless LSTM은 이전 Batch의 Network State를 유지하지 않습니다.

• Q :Keras가 Stateful LSTM과 Stateless LSTM을 구분해서 만들어 놓은 이유는 무엇인가요?

• A : LSTM에서 Stateful은 다음과 같은 의미를 가집니다.

  stateful: Boolean (default False). True인 경우에 Batch Index에서 마지막 Sample에 대한 상태는 다음 Batch Index의 초기 상태로 사용된다.

  다시 말하면, 우선 LSTM을 Train , Predict, Evaluate할 때 먼저 (nb_samples, timesteps, input_dim ) 형태의 3차원 Array 형태를 만들어야 합니다.

  이때 nb_samples의 값은 Batch Size로 나누어서 나머지가 없어야 합니다.

  예를 들어, nb_samples = 1024이고 batch_size = 64인 경우 모델은 한번에 64 개의 Sample Block을 받아서 timesetps가 얼마이건 상관없이 각 Sample Block의 출력을 계산하고 기울기의 평균을 계산한 후 전달하여 Parameter Vector를 Update합니다.

  **기본적으로 Keras는 Batch 내에서 Sample의 순서를 썪어버리기 때문에 각 Sample들 간의 시간 종속성을 잃어버리게 됩니다.

  Stateless LSTM의 경우에는 Cell State가 각 Sequence마다 Reset이 됩니다. 반면, Stateful LSTM의 경우에는 모든 State가 다음 Batch에 전달이 됩니다.

  즉, i번째 Batch에서 학습한 Cell State가 i+1번째 Batch 학습에서도 Initial State로 사용되게 된다는 의미입니다.

• Q : Keras가 Stateful LSTM에서 Input Shape 설정시에 Batch Size를 요구하는 이유는 무엇입니까?

• A : Stateless LSTM에서는 Keras가 output_dim크기만큼 State Array를 할당하며, 각 Batch를 Train한 후에 State Array는 Reset됩니다.

  Stateful LSTM에서는 이전 Batch에서의 State를 현재 Batch의 Train시에 전달합니다.

  위의 설명을 참고하면, 현재 Batch Train시에 이전 Batch의 State를 알고 있을 것입니다.

  이런 경우에 State를 저장할 구조의 Shape은 (batch_size, output_dim)가 됩니다. 이런 이유 때문에 Stateful LSTM을 만들때 Batch Size를 미리 알려주어야 합니다.

  그렇게 하지 않는다면, Keras는 Error를 낼 것입니다.

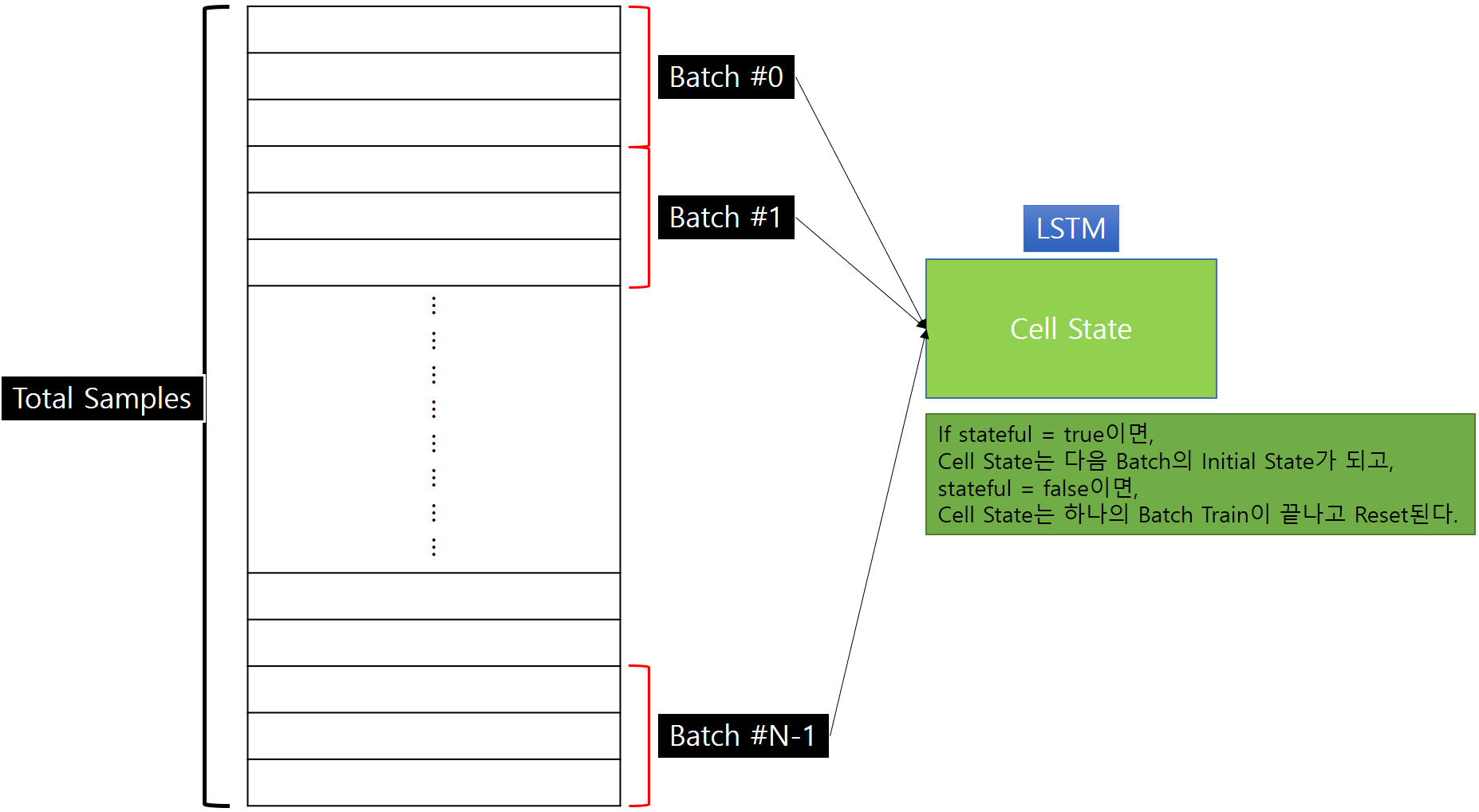
종합하면, 각 Samples들(혹은 Batch)간의 시간적인 연속성이 있는 경우에는 Stateful LSTM을 이용하는 것이 맞고,

그렇지 않은 경우에는 Stateless LSTM으로도 충분합니다.

seq_length = 1

dataX = []
dataY = []
for i in range(0, len(alphabet) - seq_length, 1):
    seq_in = alphabet[i:i + seq_length]
    seq_out = alphabet[i + seq_length]
    dataX.append([char_to_int[char] for char in seq_in])
    dataY.append(char_to_int[seq_out])
    print(seq_in, '->', seq_out)

A -> B
B -> C
C -> D
D -> E
E -> F
F -> G
G -> H
H -> I
I -> J
J -> K
K -> L
L -> M
M -> N
N -> O
O -> P
P -> Q
Q -> R
R -> S
S -> T
T -> U
U -> V
V -> W
W -> X
X -> Y
Y -> Z

# reshape X to be [samples, time steps, features]
X = numpy.reshape(dataX, (len(dataX), seq_length, 1))
X.shape

(25, 1, 1)

# normalize
X = X / float(len(alphabet))

# one hot encode the output variable
y = np_utils.to_categorical(dataY)

X.shape
y.shape

(25, 1, 1)
(25, 26)

• Stateful LSTM을 사용하기 위해서, stateful Option을 True로 설정합니다.

• Stateless LSTM의 input_shape Option 대신, Batch Size까지 같이 설정할 수 있는 batch_input_shape Option을 사용합니다.

• Stateful LSTM을 사용하여 Train할 경우에 중요한 점은 shuffle Option을 False로 설정합니다.

• 마지막으로 **Epoch마다 Model의 State를 Manual하게 Reset **시켜야 합니다.

# create and fit the model
batch_size = 1
model = Sequential()

model.add(LSTM(50, batch_input_shape=(batch_size, X.shape[1], X.shape[2]), stateful=True))

model.add(Dense(y.shape[1], activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])

for i in range(300):
    model.fit(X, y, epochs=1, batch_size=batch_size, verbose=2, shuffle=False)
    model.reset_states()

Epoch 1/1
 - 1s - loss: 3.2895 - acc: 0.0000e+00
<keras.callbacks.History at 0x1cd9f836908>

Epoch 1/1
 - 0s - loss: 3.2626 - acc: 0.0800
<keras.callbacks.History at 0x1cd9fa70f08>

(중략)

Epoch 1/1
 - 0s - loss: 0.2600 - acc: 1.0000
<keras.callbacks.History at 0x1cd9f839d88>

Epoch 1/1
 - 0s - loss: 0.2722 - acc: 1.0000
<keras.callbacks.History at 0x1cd9fa221c8>

# summarize performance of the model
scores = model.evaluate(X, y, batch_size=batch_size, verbose=0)
model.reset_states()
print("Model Accuracy: %.2f%%" % (scores[1]*100))

Model Accuracy: 100.00%

# demonstrate some model predictions
seed = [char_to_int[alphabet[0]]]

for i in range(0, len(alphabet)-1):
    x = numpy.reshape(seed, (1, len(seed), 1))
    x = x / float(len(alphabet))
    prediction = model.predict(x, verbose=0)
    index = numpy.argmax(prediction)
    print(int_to_char[seed[0]], "->", int_to_char[index])
    seed = [index]
model.reset_states()

A -> B
B -> C
C -> D
D -> E
E -> F
F -> G
G -> H
H -> I
I -> J
J -> K
K -> L
L -> M
M -> N
N -> O
O -> P
P -> Q
Q -> R
R -> S
S -> T
T -> U
U -> V
V -> W
W -> X
X -> Y
Y -> Z

# demonstrate a random starting point
letter = "K"
seed = [char_to_int[letter]]
print("New start: ", letter)

for i in range(0, 5):
    x = numpy.reshape(seed, (1, len(seed), 1))
    x = x / float(len(alphabet))
    prediction = model.predict(x, verbose=0)
    index = numpy.argmax(prediction)
    print(int_to_char[seed[0]], "->", int_to_char[index])
    seed = [index]
model.reset_states()

New start:  K
K -> B
B -> C
C -> E
E -> G
G -> H

• 예상대로 예측을 잘 하고 있습니다.

6. LSTM with Variable Length Input to One-Char Output

• 마지막으로 Stateless LSTM을 이용하여, 임의의 길이의 입력에도 다음 문자를 예측할 수 있는 Model을 만들어 보겠습니다.

• 이번에는 이전과는 약간 다른 Input Data 형태를 만들 예정입니다.

• 특별한 방법을 쓰는 것이 아니라, 가능한 많은 Case들을 만들어서 Train Data로 만드는 것입니다.

• Alphabet 26글자에 대해서 모든 길이의 Case에 대해서 Train Data를 만드는 것은 무리이므로, 여기는 1000개 정도의 임의의 Train Data만 만들것입니다.

• 먼저 Train Data 생성 함수부터 살펴보시겠습니다.

num_inputs = 1000
max_len = 5
dataX = []
dataY = []

for i in range(num_inputs):
    start = numpy.random.randint(len(alphabet)-2)
    end = numpy.random.randint(start, min(start+max_len,len(alphabet)-1))
    sequence_in = alphabet[start:end+1]
    sequence_out = alphabet[end + 1]
    dataX.append([char_to_int[char] for char in sequence_in])
    dataY.append(char_to_int[sequence_out])
    print(sequence_in, '->', sequence_out)

XY -> Z
T -> U
VWX -> Y
QRST -> U
ABC -> D
PQRST -> U
IJKLM -> N
R -> S
NO -> P
V -> W

(중략)

NOPQR -> S
BCDE -> F
X -> Y
LMNOP -> Q
JKL -> M
IJKLM -> N
IJKLM -> N
QRST -> U
NOPQ -> R
QR -> S

• 위와 같은 형태로 Random하게 Train Data를 생성합니다.

• Data가 많을수록, 겹치는 Data가 없을 수록 Model의 예측력은 더 높아지겠죠

# convert list of lists to array and pad sequences if needed
X = pad_sequences(dataX, maxlen=max_len, dtype='float32')
X.shape
X

# reshape X to be [samples, time steps, features]
X = numpy.reshape(X, (X.shape[0], max_len, 1))
X.shape
X

# normalize
X = X / float(len(alphabet))
X.shape
X

# one hot encode the output variable
y = np_utils.to_categorical(dataY)

(1000, 5)

array([[ 0.,  0.,  0., 23., 24.],
       [ 0.,  0.,  0.,  0., 19.],
       [ 0.,  0., 21., 22., 23.],
       ...,
       [ 0., 16., 17., 18., 19.],
       [ 0., 13., 14., 15., 16.],
       [ 0.,  0.,  0., 16., 17.]], dtype=float32)

(1000, 5, 1)

array([[[ 0.],
        [ 0.],
        [ 0.],
        [23.],
        [24.]],

       [[ 0.],
        [ 0.],
        [ 0.],
        [ 0.],
        [19.]],

       [[ 0.],
        [ 0.],
        [21.],
        [22.],
        [23.]],

       ...,

       [[ 0.],
        [16.],
        [17.],
        [18.],
        [19.]],

       [[ 0.],
        [13.],
        [14.],
        [15.],
        [16.]],

       [[ 0.],
        [ 0.],
        [ 0.],
        [16.],
        [17.]]], dtype=float32)

(1000, 5, 1)

array([[[0.        ],
        [0.        ],
        [0.        ],
        [0.88461536],
        [0.9230769 ]],

       [[0.        ],
        [0.        ],
        [0.        ],
        [0.        ],
        [0.7307692 ]],

       [[0.        ],
        [0.        ],
        [0.8076923 ],
        [0.84615386],
        [0.88461536]],

       ...,

       [[0.        ],
        [0.61538464],
        [0.65384614],
        [0.6923077 ],
        [0.7307692 ]],

       [[0.        ],
        [0.5       ],
        [0.53846157],
        [0.5769231 ],
        [0.61538464]],

       [[0.        ],
        [0.        ],
        [0.        ],
        [0.61538464],
        [0.65384614]]], dtype=float32)

• Stateless LSTM의 일반적인 형태로 Model을 구성하고, Train을 시작합니다.

• 이번에는 Train Data 양이 많다보니, Train에 꽤 오랜 시간이 걸립니다.

• 다른 볼 일 좀 보고 오시기 바랍니다.

batch_size = 1
model = Sequential()
model.add(LSTM(32, input_shape=(X.shape[1], 1)))
model.add(Dense(y.shape[1], activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X, y, epochs=500, batch_size=batch_size, verbose=2)

Epoch 1/500
 - 14s - loss: 3.1083 - acc: 0.0820
Epoch 2/500
 - 13s - loss: 2.8513 - acc: 0.1130
Epoch 3/500
 - 13s - loss: 2.4758 - acc: 0.1890
Epoch 4/500
 - 13s - loss: 2.2001 - acc: 0.2620
Epoch 5/500
 - 13s - loss: 2.0166 - acc: 0.3010
Epoch 6/500
 - 13s - loss: 1.8754 - acc: 0.3400
Epoch 7/500
 - 13s - loss: 1.7713 - acc: 0.3730
Epoch 8/500
 - 13s - loss: 1.6746 - acc: 0.4260
Epoch 9/500
 - 13s - loss: 1.5893 - acc: 0.4610
Epoch 10/500
 - 13s - loss: 1.5042 - acc: 0.4980
 
 (중략)
 
 Epoch 490/500
 - 13s - loss: 0.1030 - acc: 0.9920
Epoch 491/500
 - 13s - loss: 0.1046 - acc: 0.9870
Epoch 492/500
 - 13s - loss: 0.1076 - acc: 0.9890
Epoch 493/500
 - 13s - loss: 0.1073 - acc: 0.9860
Epoch 494/500
 - 13s - loss: 0.1093 - acc: 0.9830
Epoch 495/500
 - 13s - loss: 0.1089 - acc: 0.9830
Epoch 496/500
 - 13s - loss: 0.1088 - acc: 0.9840
Epoch 497/500
 - 13s - loss: 0.1423 - acc: 0.9690
Epoch 498/500
 - 13s - loss: 0.1083 - acc: 0.9840
Epoch 499/500
 - 13s - loss: 0.1032 - acc: 0.9870
Epoch 500/500
 - 13s - loss: 0.1056 - acc: 0.9840

• 정확도도 꽤 높습니다.

# summarize performance of the model
scores = model.evaluate(X, y, verbose=0)
print("Model Accuracy: %.2f%%" % (scores[1]*100))

Model Accuracy: 99.90%

• 임의의 Pattern의 예측도 잘하고 있습니다.

# demonstrate some model predictions
for i in range(20):
    pattern_index = numpy.random.randint(len(dataX))
    pattern = dataX[pattern_index]
    x = pad_sequences([pattern], maxlen=max_len, dtype='float32')
    x = numpy.reshape(x, (1, max_len, 1))
    x = x / float(len(alphabet))
    prediction = model.predict(x, verbose=0)
    index = numpy.argmax(prediction)
    result = int_to_char[index]
    seq_in = [int_to_char[value] for value in pattern]
    print(seq_in, "->", result)

['J', 'K', 'L'] -> M
['I'] -> J
['G', 'H', 'I', 'J'] -> K
['L', 'M', 'N', 'O', 'P'] -> Q
['O'] -> P
['O', 'P'] -> Q
['D', 'E', 'F'] -> G
['T', 'U', 'V', 'W', 'X'] -> Y
['K', 'L', 'M'] -> N
['A', 'B'] -> C
['P'] -> Q
['S', 'T'] -> U
['T', 'U'] -> V
['W', 'X', 'Y'] -> Z
['K', 'L', 'M'] -> N
['D', 'E', 'F', 'G', 'H'] -> I
['Q', 'R', 'S', 'T'] -> U
['B', 'C', 'D', 'E'] -> F
['D', 'E'] -> F
['F', 'G', 'H', 'I', 'J'] -> K

import matplotlib.pyplot as plt

fig, loss_ax = plt.subplots()
acc_ax = loss_ax.twinx()

loss_ax.plot(hist.history['loss'], 'y', label='train loss')
#loss_ax.plot(hist.history['val_loss'], 'r', label='val loss')
loss_ax.set_xlabel('epoch')
loss_ax.set_ylabel('loss')
loss_ax.legend(loc='upper left')

acc_ax.plot(hist.history['acc'], 'b', label='train acc')
#acc_ax.plot(hist.history['val_acc'], 'g', label='val acc')
acc_ax.set_ylabel('accuracy')
acc_ax.legend(loc='upper left')

plt.show()

• 이상으로 LSTM을 이용해서 Alhpabet 문자를 예측하는 Model을 다양한 형태로 만들어 보았습니다.

• 다음 Post에서는 Time Series Data를 이용한 다양한 LSTM Model을 살펴보도록 하겠습니다.