Backpropagation
이번 Post에서는 Backpropagation에 관해서 알아보도록 하겠습니다.
0. Introduction
Backpropagation은 Deep Learning 학습의 핵심 메커니즘입니다.
Deep Learning의 학습은 학습하려는 Train Data를 Network에 넣어서 값을 출력하는 순서를 거치게 됩니다.
이 과정을 Feedforward라고 합니다. 물론 이 과정에서 출력되는 값은 Network이 학습이 진행되기 전이기 때문에 실제 Target 값과 많이 차이가 나게 됩니다.
Deep Learning은 Target 값과 실제 정답과의 차이를 이용하여 Network을 구성하는 Parameter(Weight , Bias)를 적절하게 Update 합니다.
이 과정을 Backpropagation이라고 하며, 이번 Post에서는 Backpropagation 과정이 실제로 어떻게 동작하는지 알아보겠습니다.
1. Feedforward
먼저, Train Data로 Network이 Target 값을 계산하는지 알아보겠습니다.
다음과 같은 Network이 있다고 해보겠습니다. 매우 Simple한 구조지만, 모든 Network은 이 구조의 확장이기 때문에 설명하는데 충분하다고 생각합니다.
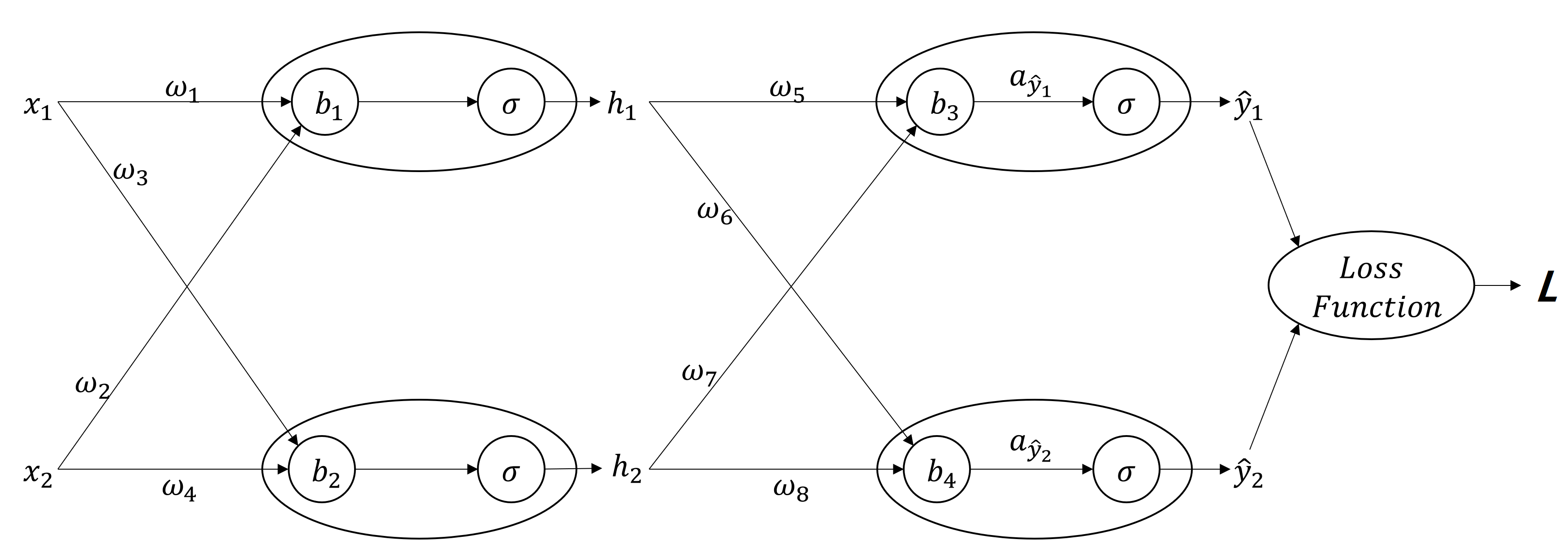
Activation Function은 Sigmoid라고 가정하겠습니다. 아시다시피 Sigmoid의 수식은 아래와 같습니다.
Loss Function은 MSE(Mean Squared Error)라고 가정하겠습니다. MSE를 구하는 수식은 아래와 같습니다.
먼저, 첫번째 Activation Function을 통과한 $ℎ_1=𝜎(𝑥_1𝑤_1+𝑥_2 𝑤_2+𝑏_1)$이고, $ℎ_2=𝜎(𝑥_1𝑤_3+𝑥_2𝑤_4+𝑏_2)$가 됩니다.
그리고, 두번째 Activation Function을 통과한 $𝑦_1=𝜎(ℎ_1𝑤_5+ℎ_2𝑤_7+𝑏_3)$이고, $𝑦_2=𝜎(ℎ_1𝑤_6+ℎ_2𝑤_8+𝑏_4)$가 됩니다.
2. Backpropagation
입력값 $x_1,x_2$ 가 신경망을 거쳐서 출력값 $\hat{𝑦_1}, \hat{𝑦_2}$가 계산되어 나왔습니다.
이 $\hat{𝑦_1}, \hat{𝑦_2}$가 실제 Target Value인 $𝑦_1, 𝑦_2$와 얼마나 차이가 나느냐 계산해서 이 차이만큼 신경망의 parameter(w,b)들을 update 시켜야 합니다.
이 동작의 반복을 ‘학습’이라고 합니다.
2.1. Loss Function
다양한 Loss Function이 존재하고 상황에 맞는 Loss Function을 선택해야 합니다.
이 Post에서는 가장 심플하다고 할 수 있는 MSE를 선택하기로 했습니다.
MSE는 신경망 출력값과 실제 Target 값의 차이를 구해서 제곱한 후 평균을 구하는 방식을 취합니다.
2.2. 편미분
Loss Function을 통해 실제값과 신경망이 구한 값의 차이, 즉, 에러 신호를 구했으면 이 에러신호가 신경망의 어떤 Parameter에 의해서 얼마나 영향을 받는지를 확인해서 신경망의 Parameter를 Update해 주어야 합니다.
구체적으로, 에러 신호를 Feedforward의 반대 방향으로 넘어가면서(Backpropagation) 편미분을 통해서 특정 Parameter가 에러 신호에 어느 정도 영향을 주는지 계산(미분)해서 개별적으로 Parameter를 에러 신호가 줄어드는 방향으로 Update해 나가는 동작을 반복하게 됩니다.
3. Example of Backpropagation
실제 편미분을 이용해 Parameter를 Update하는 방법을 알아보겠습니다.
먼저 Backpropagation은 Feedforward를 구성하는 각 Function들의 미분을 해야 하기 때문에,
Activation Function와 Loss Function의 도함수부터 먼저 알아보도록 하겠습니다.
3.1. Activation Function의 도함수
앞서 살펴봤듯이, Sigmoid의 형태는 아래와 같습니다.
Sigmoid의 도함수는 다음과 같습니다.
3.2. Loss Function의 도함수
우리는 Loss Function으로 MSE를 사용하기로 했으며, 수식은 아래와 같습니다.
MSE의 도함수의 형태는 아래와 같습니다.
도함수를 구하는 구체적인 순서는 생략하기로 하겠습니다.
3.3. Overall Process
Backpropagation의 전체적인 순서는 Feedforward에서 구한 Loss를 뒤로 넘기면서 각 Parameters(w,b)를 Loss가 줄어드는 방향으로 Update해 나가는 것입니다.
이제부터는 각 단계별로 Backpropagation이 실제로 적용되어 계산되는 방식을 알아보도록 하겠습니다.
3.4. Loss Function 단계
Loss Function은 MSE 방식을 사용했으니, MSE의 도함수를 이용해서 L을 Backpropagation합니다.
앞에서 알아본 MSE의 도함수를 이용해서 결과를 구하면
가 됩니다.
3.5. Activation Function 단계
Activation Function은 Sigmoid로 선택하였고, 앞서 Sigmoid의 도함수의 형태는
라는 것도 알아보았습니다.
여기서 $x=a_{\hat{𝑦_i}}$가 되고, $𝜎(a_{\hat{𝑦_i}})$는 곧 $\hat{y_i}$ 가 됩니다.
정리하면,
가 됩니다.
여기까지 결과를 Chain-Rule로 정리하면, 두번째 Hidden Layer의 출력값이 Loss에 미치는 영향을 에러 신호 $𝛿_{\hat{𝑦_i}}$ 라고 정의하면,
가 됩니다.
3.6. Parameter Update
에러 신호 $𝛿_{\hat{𝑦_i}}$를 구했으니, 이 값을 바탕으로 w,b를 Update합니다.
실제 w,b 계산 방법은 아래와 같습니다.
여기서 “η”는 Learning Rate값을 나타냅니다.
이 단계에서 Optimizer가 적용이 되는데, 선택한 Optimizer의 알고리즘에 따라서 “η”(Learning Rate)값에 따라서 Weight/Bias 값을 조절하게 됩니다.
$𝑤_6,𝑤_8, 𝑏_4$도 에러 신호 $𝛿_{\hat{𝑦_i}}$를 이용해서 동일한 방식으로 구할 수 있습니다.
3.7. Hidden Layer의 에러 신호
이 부분부터는 이전의 계산하는 방식과는 다른 방법을 이용해서 진행합니다.
앞의 단계에서는 전체 신경망의 최종결과 값인 Loss를 알고 있기때문에 오차, 즉 에러 신호를 계산할 수 있었습니다.
하지만, Hidden Layer에서는 실제 값을 모르고 알 수 있는 것은 단지 Backpropagation으로 전달된 에러 신호 $𝛿_{\hat{𝑦_i}}$뿐입니다.
우리는 첫번째 Hidden Layer의 출력 $ℎ_𝑖$의 에러 신호 $𝛿_{h_i}$ 를 구하려고 합니다.
에러 신호 $𝜹_{𝒉_𝒊}$는 생각해 보면 신경망을 거쳐 결국 $𝛿_{𝑦_𝑖}$에 영향을 끼치기 때문입니다.
그래서, $𝛿_{𝑦_𝑖}$를 Target으로 생각하고 이전과 유사하게 계산하면 됩니다.
동일한 방식으로 $𝛿_{ℎ_2}$도 구할 수 있습니다.
이제 에러 신호를 구했으니, 이 값을 바탕으로 $𝑤_1$ ~ $𝑤_4$ , $𝑏_1$ ~ $𝑏_2$도 Update할 수 있습니다.
4. Summary
앞서 살펴본 Feedforward & Backpropagation 과정을 전체 Dataset에 대해서 반복해서 적용하면서 Loss가 작아지는 방향으로 Parameters(W,B)를 Update하는 과정을 ‘학습(Training)’이라고 합니다.
Backpropagation은 Loss값을 뒤로 넘기면서 개별 Parameters(W,B)가 Loss에 얼마나 많은 영향을 미치는가를 편미분을 통해서 파악하고, 이 값을 Loss가 작아지는 방향으로 Update하는 과정입니다.
Deep Learning 학습에 Backpropagation이 사용된다고 알고는 있지만 실제 어떻게 동작하는지 정리해 볼 필요가 있을 것 같아서 나름대로 정리를 해 보았으니, 도움이 되셨다면 좋겠습니다.